Cara Menghitung Median Data Kelompok untuk Data Tabel Frekuensi

Dalam melakukan penyajian data. maka tidak bisa lepas dari ukuran pemusatan data yang merupakan suatu nilai yang didapat dari kumpulan data yang dipakai untuk mewakili keseluruhan data yang ada. Ukuran pemusatan data ini terdiri dari mean, median, modus.
Dilansir dari Sampoerna Academy, median atau kuartil adalah nilai tengah dari sekumpulan data yang sudah diuraikan sebelumnya dari data terkecil hingga terbesar atau sebaliknya.
Median banyak digunakan dalam pengolahan data, misalnya menentukan nilai ulangan dimana median akan muncul bila ada pembagian kelas menjadi dua kelompok berdasarkan urutan nilai.
Median memiliki dua jenis yaitu median data tunggal dan media data kelompok. Ulasan berikut, akan membahas median data kelompok termasuk cara menghitungnya. Simak penjelasan di bawah ini.
Pengertian Median Data Kelompok
Median data kelompok merupakan jenis data median yang biasanya disajikan dalam bentuk tabel frekuensi dan telah dikelompokkan dalam kelas interval secara matematis. Selain itu, pada median data kelompok biasanya terdapat jarak dari data satu ke data yang lain.
Untuk mengetahui nilai median pada data kelompok, Anda harus mengetahui frekuensi kumulatifnya agar dapat mengolah data tersebut sehingga lebih mudah dikerjakan nantinya.
Cara Menghitung Median Data Kelompok
Untuk melakukan cara ini, Anda perlu mengetahui terlebih dahulu kelas mediannya. Caranya adalah dengan mencari kelas data yang memuat nilai tengah.
Dalam menghitung median data kelompok, Anda harus mencari beberapa poin penting yaitu tepi bawah kelas median, banyaknya data, frekuensi kumulatif sebelum kelas median, frekuensi kelas median, dan panjang kelas.
Adapun rumus yang digunakan adalah
Me = Tb + [1/2 n – f kum] I / fm
Keterangan :
Tb = Tepi bawah kelas median – p
P = 0,5
I = Interval
n = jumlah frekuensi
f kum = jumlah frekuensi sebelum kelas median
fm = frekuensi sebelum kelas median
Jika nilai dinyatakan dalam bilangan bulat dan p= 0,05 jika nilai dinyatakan dalam bilangan desimal 1 angka di belakang koma.
Contoh Soal
Berikut ini beberapa contoh soal yang diambil dari berbagai sumber agar Anda lebih paham cara menghitung median data kelompok.
Contoh Soal 1
Sebuah pendataan dilakukan oleh sekelompok peneliti untuk mengetahui tinggi badan siswa kelas 1. Hitunglah mean dari data kelompok tinggi badan siswa kelas 1 SDN Bahagia Selalu jika diperoleh data seperti berikut ini:
1. Interval 100-110, dengan frekuensi 12
2. Interval 120-130, dengan frekuensi 18
3. Interval 140-150, dengan frekuensi 10
Pembahasan:
Pertama, kita jumlahkan semua frekuensi yang ada
Jumlah frekuensi = 12 + 18 + 10 = 40
Kedua, tentukan kelas median :
Kelas median adalah data yang mengandung ke-n/2
Maka, kelas media = 40/2= 20
Kelas median ditunjukkan oleh data ke- 20 di mana itu terletak di kelompok ke-2 pada frekuensi ke 2 yang berjumlah frekuensi adalah 30.
Kelompok : ke-2
Interval : 120-130
Pada f sebelum f kelas median = 12
Frekuensi sebelum kelas median (fkum)
Fkum = 12
Sementara frekuensi di mana kelas median berada di fm
Fm= 18
Jarak interval l = 10
Oleh karena datanya dinyatakan dalam bilangan bulat, maka tepi bawah kelas mediannya adalah sebagai berikut.
Nilai bawah dari kelompok ke-3
Interval 120 – 130 adalah 120
Tb = 120-p
Karena bilangan bulat maka p= 0,5
Tb = 120 – 0,5 = 119,5
Dengan demikian, mediannya dirumuskan sebagai berikut.
Me = Tb+ [ ½ n- fkum] l / fm
Me = 119,5 + [ ½ 20- 12 ]. 10 / 10
Me = 119,5 + [10 – 12 ,] 10 / 10
Me = 119,5 + (-2).10 / 10
Me = 119,5 – 20 / 10
Me = 119,5 – 2
Me = 117,5
Jadi, median dari data tersebut adalah 117,5
Contoh Soal 2
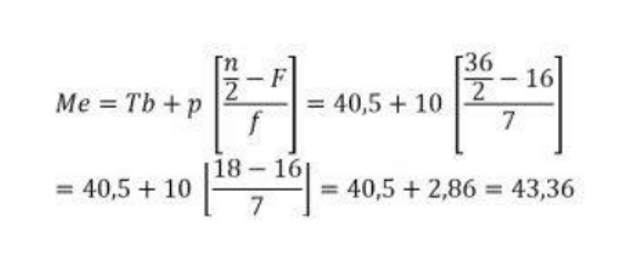 Ilustrasi Penyelesaian Soal Median Data Kelompok. Foto : buku Bahan Ajar Matematika Materi Statistika (Median)
Ilustrasi Penyelesaian Soal Median Data Kelompok. Foto : buku Bahan Ajar Matematika Materi Statistika (Median)
Contoh Soal 3
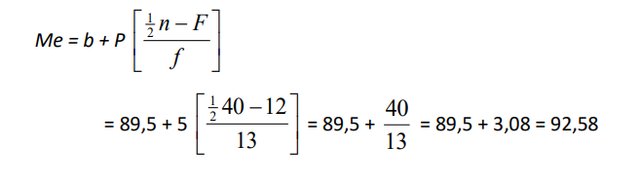
Contoh Soal 4

 Sehingga median berat badan mahasiswa adalah 64,5 kg.
Sehingga median berat badan mahasiswa adalah 64,5 kg.




