Pengertian, Rumus, dan Contoh Soal Hukum Faraday

31 Oktober 2023, 12:14

Freepik

Ilustrasi, arus listrik.

Hukum Faraday adalah salah satu prinsip dasar dalam elektromagnetisme yang ditemukan oleh ilmuwan Inggris bernama Michael Faraday. Hukum ini menyatakan bahwa perubahan medan magnet di sekitar suatu kumparan kawat akan menginduksi arus listrik dalam kawat tersebut.

Hukum Faraday dinyatakan dalam dua bentuk utama, yakni Hukum Faraday Induksi Elektromagnetik dan Hukum Faraday Induksi Elektromagnetik Lenz.

Hukum Faraday merupakan prinsip yang sangat penting dalam ilmu elektromagnetisme dan memainkan peran sentral dalam perkembangan teknologi modern dan pemahaman manusia tentang interaksi antara medan magnetik dan arus listrik.

Circuit breaker di SUTET Muara Tawar, Bekasi, Jawa Barat. (Kementerian BUMN)

Rumus Hukum Faraday

Hukum Faraday dibagi menjadi dua, yaitu hukum Faraday 1 dan hukum Faraday 2. Kedua hukum ini memiliki bunyi dan rumus yang berbeda, antara lain sebagai berikut.

1. Rumus Hukum Faraday 1

Bunyi hukum Faraday 1:

“Massa zat yang dilepaskan selama elektrolisis berbanding lurus dengan jumlah listrik yang digunakan”

Berdasarkan bunyinya, rumus hukum Faraday 1 dapat dituliskan sebagai berikut.

G ≈ Q atau G ≈ it

Keterangan:

G = massa yang dihasilkan pada elektrolisis (gram)

i = arus listrik (ampere)

t = waktu (detik)

Q = muatan listrik dalam sel (Coulomb)

2. Rumus Hukum Faraday 2

Bunyi hukum Faraday II:

“Massa zat yang dilepaskan pada elektrolisis berbanding lurus dengan massa ekuivalen zat itu”

Berdasarkan bunyi hukum Faraday 2 tersebut, maka rumusnya adalah:

Keterangan:

ME = massa ekivalen

x = jumlah elektron yang diterima atau dilepaskan

Jika rumus hukum Faraday 1 dan 2 ini digabungkan, maka akan diperoleh rumus baru, yaitu:

G = k . i . t . ME

Keterangan:

k = tetapan/faktor pembanding

Faraday menemukan bahwa harga faktor pembanding ini adalah 1/96.500, sehingga rumus di atas dapat dituliskan sebagai berikut.

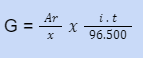
di mana :

G = massa yang dihasilkan pada elektrolisis (gram)

i = arus listrik (ampere)

t = waktu (detik)

ME = massa ekivalen

Ar = massa atom relatif

x = jumlah elektron yang diterima atau dilepaskan

Contoh Soal Hukum Faraday

Berikut ini sepuluh contoh soal hukum Faraday dari berbagai sumber yang bisa dipelajari agar paham cara menerapkan rumusnya dengan baik dan benar.

Contoh Soal 1

Hitunglah massa tembaga yang dihasilkan jika arus listrik sebesar 10 ampere dialirkan selama 9.500 detik ke dalam larutan C_uSO₄ (Ar Cu= 63,5)!

Pembahasan

Reaksi pengendapan Cu:

Cu²⁺_(aq) + 2e → Cu_(s)

Maka, massa Cu yang dihasilkan adalah:

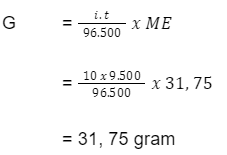
Jadi, massa tembaga yang dihasilkan adalah sebesar 31,75 gram.

Contoh Soal 2

Apabila dalam rangkaian di atas membentuk endapan Cu sebesar 5 gram, maka berapa Ag yang mengendap pada elektrode? (Cu = 63,5, Ag= 108).

Jawab:

Untuk menghitung massa Ag, wag menggunakan rumus yang sudah disediakan pada gambar di atas di mana ME = Ar / biloks. Sementara diketahui bahwa Cu, wcu = 5 gram. Untuk menghitung MEcu dan MEag harus menuliskan dulu reaksi reduksi Cu dan Ag seperti gambar di bawah ini.

Jika hukum Faraday I dan Faraday II digabungkan maka diperoleh w = I x t x ME, selanjutnya perbandingan ini menjadi persamaan dengan menambahkan faktor 1/96.500 dan diperoleh rumus hukum Faraday w= 1/96.500 x I x t x ME.

Contoh Soal 3

Sebuah kumparan terdiri dari 50 lilitan, fluks magnet dalam kumparan berubah sebesar 5 x 10^-3 weber dalam selang waktu 10ms (milidetik). Hitunglah Gaya Gerak Listrik atau GGL induksi pada kumparan tersebut!

Penyelesaian:

Jumlah Lilitan (N) = 50
Selang waktu (Δt) = 10ms = 10 x 10^-3 second
ΔΦ = 5 x 10^-3 weber
GGL induksi (ɛ ) = ???

Jawaban :

ɛ = -N (ΔΦ/∆t)
ɛ = -50 (5 x 10^-3 wb / 10 x 10^-3)
ɛ = -50 (0,5)
ɛ = -25V

Jadi, Gaya Gerak Listrik Induksinya adalah -25V.

Contoh Soal 4

Berapa emas dan klor yang terbentuk, jika arus listrik 10 A melewati larutan emas(III) klorida selama 6 menit? (Ar Au = 196,73; Ar Cl = 35,45). Diketahui reaksi pada elektrode:

Katode: Au3+(aq) + 3e– → Au(s)

Anode: 2Cl– (aq) → Cl2(g) + 2e–

Pembahasan

Massa ekuivalen Au adalah 196,73 / 3 = 65,66 gram

Massa ekuivalen Cl₂adalah 35,45 / 1 = 35,45 gram

Au yang terbentuk

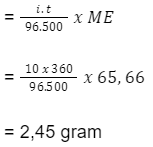
Cl₂ yang terbentuk

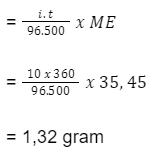
Jadi, emas yang terbentuk adalah 2,45 gram, sedangkan klor yang terbentuk adalah 1,32 gram.

Contoh Soal 5

Arus listrik sebesar 0,2 ampere dialirkan selama 50 menit ke dalam elektrolisis dengan kandungan larutan CuCl2. Berapa endapan Cu pada katode? (Ar Cu=63,5)

Jawaban:

Arus, I = 0,2 A;

Waktu, t = 3.000 detik

Cu2+(aq) + 2e– → Cu(s)

ME Cu = Ar/x

= 63,5/2 = 31,75

G = (1/96.500) x 0,2 A x 3.000 detik x 31,75

= 0,197 g.

Contoh Soal 6

Berapa waktu yang diperlukan untuk mengendapkan 5,60 gram besi dalam larutan besi (III) klorida dengan arus 5 A? (Ar Fe = 55,85). Diketahui reaksi pada katode:

Fe³⁺_(aq) + 3e^– → Fe_(s)

Massa ekuivalen Fe adalah 55,85 / 3 = 18,62 gram

Jadi, waktu yang diperlukan untuk mengendapkan 5,60 gram besi dalam larutan besi (III) klorida dengan arus 5 A adalah 5.804 detik.

Sutet PLN ( ANTARA FOTO/Prasetia Fauzani)

Contoh Soal 7

Hitunglah massa tembaga dari arus listrik sebesar 10 ampere yang dialirkan selama 9650 detik ke dalam larutan CuSO4 (Ar Cu = 63,5)!

Jawaban:

Reaksi pengendapan Cu = Cu2 + (aq) + 2e -> Cu(s)

ME Cu = Ar / x

ME Cu = 63,5 / 2

ME Cu = 31,75

Maka massa Cu yang dihasilkan adalah

G = (i x t / 96500) x ME

G = (10 x 9650 / 96500) x 31,75

G = 31,75 gram

Contoh Soal 8

Pada dua sel elektrolisis yang disusun seri dengan elektroda inert terdiri dari larutan NiSo4 dan ZnSO4 dialirkan arus listrik sebesar 6 ampere selama 1 jam. Pada elektrolisis tersebut dihasilkan 6,54 gram endapan Ni.

Hitung massa endapan yang dihasilkan di katoda pada sel elektrolisis yang kedua (Ar Zn = 65, Ni = 58,5)!

Jawab:

Reaksi pengendapan Ni adalah Ni2 (aq) + 2e -> Ni(s)

Reaksi pengedapan Zn adalah Zn2 (aq) + 2e -> Zn(s)

Me Ni = Ar / x

Me Ni = 58,5 /2

Me Ni = 29,25

Me Zn = Ar / x

Me Zn = 65 / 2

Me Zn = 32,5

Maka massa Zn yang dihasilkan adalah

G Ni / G Zn = Me Ni / Me Zn

6,54 / G Zn = 29,25 / 32,5

G Zn = 7,26 gram

Contoh Soal 9

Sebuah kawat melintang di dalam medan magnetik dengan fluks magnetik yang melalui kawat tersebut berubah sebesar 0,02 T·m²/s. Jika gaya elektromotorik (EMF) yang diinduksi dalam kawat tersebut adalah 5 V, apa resistansi kawat tersebut?

Jawaban:
Dalam soal ini, kita diberikan perubahan fluks magnetik (dΦ/dt) sebesar 0,02 T·m²/s dan gaya elektromotorik (EMF) (Ε) sebesar 5 V. Kita akan menggunakan persamaan Ε = -dΦ/dt untuk mencari EMF. Namun, informasi tentang resistansi (R) tidak diberikan secara langsung. Kita akan menggunakan persamaan Ι = Ε/R untuk mencari resistansi.

Langkah 1: Hitung resistansi (R)
Ι = Ε/R
R = Ε/Ι
R = 5 V / Ι

Langkah 2: Menggunakan persamaan Ε = -dΦ/dt
Ε = -0,02 T·m²/s

Langkah 3: Menggabungkan kedua persamaan untuk mencari resistansi
R = 5 V / Ι = 5 V / (-0,02 T·m²/s)

Contoh Soal 10

Berapakah massa ekuivalen untuk sebuah reaksi berikut Cu2+ (aq) + 2e – Cu (s) jika memiliki, tembaga (Cu) Ar = 63,5 ?

Dilihat dari reaksi di atas maka terlihat adanya perubahan bilangan oksidasi yakni pada +2, sehingga massa ekuivalen dari Cu adalah ME = Ar/biloks = 63,5/2 = 31,75.

Apabila jumlah listrik yang sama dialirkan ke dalam dua atau lebih sel elektrolisis dengan elektrolit berbeda. Maka perbandingan zat yang dibebaskan berbanding lurus dengan perbandingan massa ekuivalen zat.

Editor: Agung

Pengertian, Rumus, dan Contoh Soal Hukum Faraday