Memahami Rumus Luas Permukaan Balok Beserta Contoh Soalnya
Dalam mata pelajaran matematika SMP, siswa akan mempelajari tentang berbagai bangun ruang termasuk balok.
Adapun dalam materi balok ini, terdapat pula pokok bahasan mengenai rumus luas permukaan balok yang ditujukan untuk mengetahui jumlah keseluruhan luas dan sisi pada suatu bidang ruang balok.
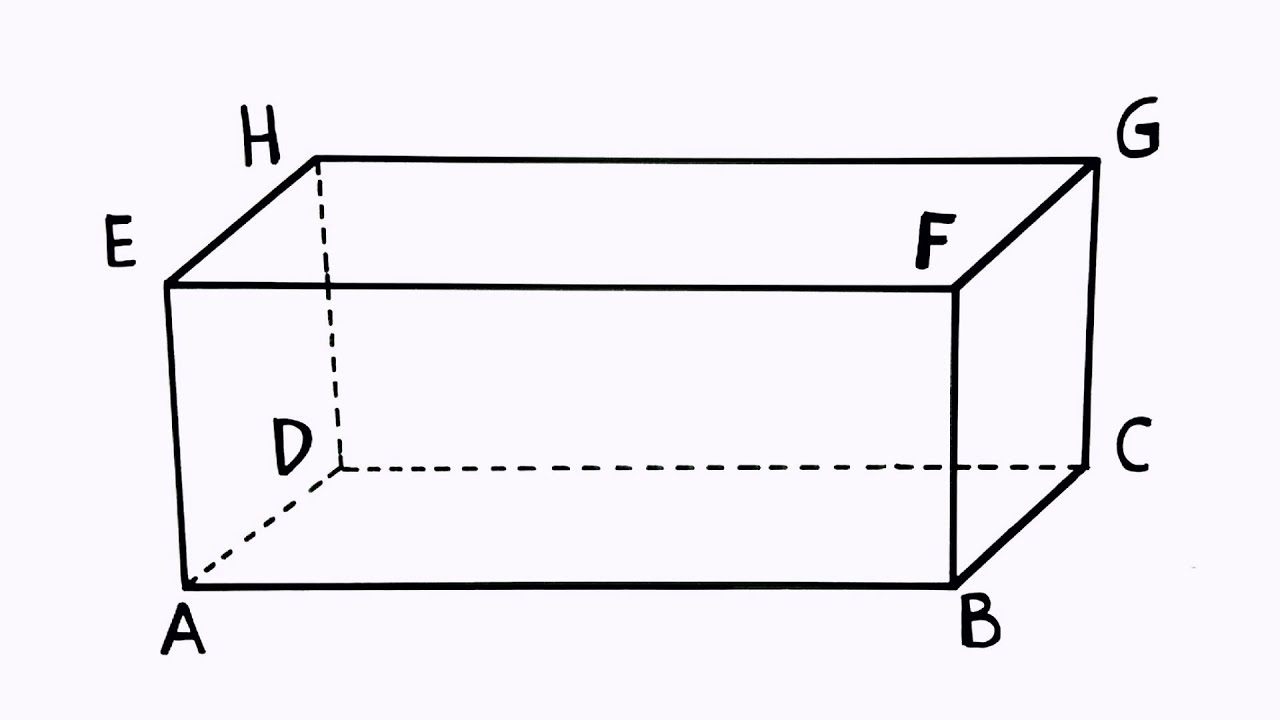
Balok sendiri dapat didefinisikan sebagai bangun ruang yang memiliki tiga pasang sisi berhadapan yang sama bentuk dan ukurannya, di mana setiap sisinya berbentuk persegi panjang.
Pada balok juga terdapat 3 pasang sisi-sisi yang sama panjang, yaitu panjang (p), lebar (l), dan tinggi (t).
Pada artikel ini, akan dibahas lebih mendalam mengenai rumus luas permukaan balok beserta contoh soalnya yang bisa dipelajari. Berikut di bawah ini rangkumannya.
Rumus Luas Permukaan Balok
Dikutip dari buku berjudul TOP No. 1 UN SMP/MTs 2016 Seri Pendalaman Materi yang ditulis oleh Tim Guru Indonesia, berikut ini rumus luas permukaan balok:
L = 2 x [(p x l) + (p x t) + (l x t)]
Keterangan:
L = luas permukaan balok
p = panjang balok
l = lebar balok
t = tinggi balok
Contoh Soal Luas Permukaan Balok
Berikut di bawah ini 12 contoh soal dari berbagai sumber yang bisa dipelajari agar lebih paham penggunaaan rumus luas permukaan balok.
Contoh Soal 1
Jika panjang rusuk balok mainan milik Sinta AB = 20 cm, BC = 10 cm, dan BF = 5 cm. Maka, berapa luas permukaan balok tersebut?
Jawab:
L = 2 x [(p x l) + (p x t) + (l x t)]
= 2 x [(20 x 10) + (20 x 5) + (10 x 5)]
= 2 (200 + 100 + 50)
= 2 (350)
= 700 cm²
Contoh Soal 2
Sebuah balok memiliki panjang 18 cm, lebar 12 cm, dan tinggi 9 cm. Luas permukaan balok tersebut adalah...
Jawab:
L = 2 x [(p x l) + (p x t) + (l x t)]
= 2 x [(18 x 12) + (18 x 9) + (12 x 9)
= 2 (216 + 162 + 108)
= 2 (486)
= 972 cm²
Contoh Soal 3
Sebuah balok memiliki lebar 5 cm dan tinggi 3 cm. Jika luas permukaannya adalah 142 cm², berapa panjang balok tersebut?
Jawab:
L = 2 x [(p x l) + (p x t) + (l x t)]
142 = 2 x [(p x 5) + (p x 3) + (5 x 3)]
142 = 2 (5p + 3p + 15)
142 = 2 (8p + 15)
142/2 = 8p + 15
71 = 8p + 15
71 - 15 = 8p
56 = 8p
p = 7 cm
Contoh Soal 4
Sebuah balok memiliki ukuran panjang 200 cm, lebar 2 cm dan tinggi 10 cm. Berapakah luas permukaan dari balok tersebut?
Jawaban:
L = 2 x (p . l + p. t + l. t)L = 2 x (200 x 2 + 200 x 10 + 2 x 10)
L = 2 x (400 + 2.000 + 20)
L = 2 x (2.420) L = 4.840 cm2
Contoh Soal 5
Sebuah balok memiliki ukuran panjang 12 cm, lebar 7 cm, dan tinggi 5 cm. Berapakah luas permukaan dari balok tersebut?
Jawaban:
L = 2 x (p . l + p. t + l. t)L = 2 x (12 x 7 + 7 x 5 + 12 x 5)
L = 2 x (84 + 35 + 60)
L = 2 x (179) L = 358 cm²
Contoh Soal 6
Sebuah balok memiliki panjang, lebar, dan tinggi secara urut adalah 8 cm, 6 cm, dan 4 cm. Hitung dan temukan luas permukaan balok tersebut!
Penyelesaian:
Diketahui: p = 8 cm, l = 6 cm, dan t = 4 cm
Jawaban: 2 (pl + pt + lt) = 2(8 x 6 + 8 x 4 + 6 x 4) = 208
Jadi, luas permukaan balok tersebut adalah 208 cm persegi.
Contoh Soal 7
Apabila panjang rusuk balok mainan milik Sita adalah AB = 20 cm, BC = 10 cm, dan BF = 5 cm, maka berapa luas permukaan balok mainan tersebut?
Penyelesaian:
Luas permukaan balok (L)
= 2(p x l + p x t + l x t)
= 2 (20 x 10 + 20 x 5 + 10 x 5)
= 2 (200 + 100 + 50) = 700
Jadi, luas permukaan balok mainan tersebut adalah 700 cm persegi.
Contoh Soal 8
Sebuah ruang balok memiliki panjang 10 cm, lebar 8 cm, dan tinggi 5cm. Cari dan temukan luas permukaan balok tersebut!
Penyelesaian:
Luas permukaan balok (L)
= 2(p x l + p x t + l x t)
= 2[(10 x 8 ) + (10 x 5) + (8 x 5)
= 2(80 + 50 + 40)
= 2 x 170
= 340 cm persegi
Jadi, luas permukaan balok tersebut adalah 340 cm persegi.
Contoh Soal 9
Berapakah luas permukaan balok yang memiliki panjang 12 cm, lebar 7 cm, dan tinggi 8 cm?
Jawaban:L = 2 × (pl + lt + pt)
L = 2 x (12 x 7 + 12 x 8 + 7 x 8)
L = 2 x (84 + 96 + 54)
L = 2 x 236
L = 472 cm²Jadi, luas permukaan balok tersebut adalah 472 cm².
Contoh Soal 10
Lebar dan tinggi sebuah balok berturut-turut adalah 3 cm dan 2 cm. Jika luas permukaannya 62 cm², berapakah panjang balok tersebut?
Jawaban:
L = 2 × (pl + pt + lt)
62 = 2 ×(3p + 2p + [2×3])
62/2 = 3p + 2p + 6
31 - 6 = 5p
25 = 5p
p = 5
Jadi, panjang balok tersebut adalah 5 cm, jika rumus luas permukaan balok 62 cm².
Contoh Soal 11
Sebuah kardus memiliki bentuk balok dengan panjang 30 cm, lebar 20 cm, dan tinggi 10 cm. Berapa luas permukaan kardus tersebut?
Pembahasan:
Untuk menyelesaikan masalah ini, kita dapat menggunakan rumus luas permukaan balok, yaitu 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi). Dalam hal ini, panjang kardus adalah 30 cm, lebar kardus adalah 20 cm, dan tinggi kardus adalah 10 cm. Oleh karena itu, luas permukaan kardus dapat dihitung sebagai berikut:
Luas permukaan = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
= 2 x (30 cm x 20 cm + 30 cm x 10 cm + 20 cm x 10 cm)
= 2 x (600 cm2 + 300 cm^2 + 200 cm) = 2 x 1100 cm = 2200 cm
Jadi, luas permukaan kardus tersebut adalah 2.200 cm
Contoh Soal 12
Sebuah balok memiliki ukuran panjang 12 cm, lebar 7 cm, dan tinggi 5 cm. Berapakah luas permukaan dari balok tersebut?
Jawab:
L = 2 x (p . l + p. t + l. t)
L = 2 x (12 x 7 + 7 x 5 + 12 x 5)
L = 2 x (84 + 35 + 60)
L = 2 x (179) L = 358 cm²