Memahami Rumus Teorema Pythagoras Beserta Contoh Soal Sebagai Bahan Belajar

Teorema Pythagoras merupakan salah satu materi matematika yang umumnya dipelajari di kelas 8 SMP. Namun tidak jarang juga materi ini telah diajarkan sejak kelas 4 SD.
Dilansir dari laman Ruangguru, teorema pythagoras adalah teorema yang menjelaskan hubungan panjang sisi pada segitiga siku-siku. Oleh karena itu, teorema ini hanya berlaku untuk segitiga siku-siku saja.
Dalam materi ini, kuadrat sisi miring segitiga siku-siku adalah jumlah kuadrat kedua sisi lainnya.
Untuk lebih memahami materi ini, berikut di bawah ini ulasan mengenai rumus teorema pythagoras dan contoh soalnya yang bisa dipelajari.
Rumus Teorema Pythagoras
Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi yang pendek (kaki tegak dan kaki samping).
Berdasarkan penjelasan dari buku Rumus Lengkap Matematika SMP karya Drs. Joko Untoro, berikut rumus phytagoras:
Dalam bentuk matematis, rumus pythagoras dapat ditulis sebagai:
c² = a² + b²
di mana c adalah panjang hipotenusa, dan a dan b adalah panjang kedua sisi yang pendek
Rumus diatas digunakan untuk mencari sisi miring atau sisi terpanjang pada segitiga siku-siku.
Untuk mencari sisi depan dan sisi sampingnya, rumus yang digunakan, yaitu:
a² = c² - b² (untuk mencari sisi depan)
b² = c² - a² (untuk mencari sisi samping)
Perlu diingat, dalam menentukan persamaan phytagoras, perlu diperhatikan siapa yang berkedudukan sebagai sisi miring dari segitiga siku-siku. Selain itu, akan lebih cepat juga untuk mencari sisi yang ditanya jika menghafalkan triple pythagoras.
Berikut ini beberapa pola dari triple phytagoras:
- 3, 4, 5
- 5, 12, 13
- 6, 8, 10
- 7, 24, 25
- 8, 15, 17
- 9, 40, 41
- 11, 60, 61
- 12, 35, 37
- 13, 84, 85
- 13, 84, 85
Contoh Soal Teorema Pythagoras
Agar lebih mudah memahami penggunaan rumus teorema pythagoras, berikut ini sepuluh contoh soal dan pembahasannya yang telah dirangkum dari berbagai sumber.
Contoh Soal 1
Sebuah segitiga siku-siku diketahui memiliki sisi alas (a) 6 cm dan sisi miring (c) 10 cm. Hitung dengan rumus Pythagoras tinggi (b) dari segitiga siku-siku ini.
Jawab:
a= 6 cm
c= 10 cm
b= ?
Berikut cara mencari tinggi (b) segitiga siku-siku dengan menggunakan rumus Pythagoras.
c2= a2 + b2
b2= c2 - a2
b2= 102 - 62
b2= 100 - 36b2= 64
b= √64
b= 8 cm
Contoh Soal 2
Suatu segitiga siku- siku memiliki sisi tegak (AB) panjangnya 15 cm ,dan sisi mendatarnya (BC) 8 cm, berapa cm sisi miringnya (AC)?
Pembahasan
Diketahui:
AB = 15
BC = 8
Ditanya:
Panjang AC?
Jawab:
AC2 = AB2 + BC2
AC2 = 152 + 82
AC2 = 225 + 64
AC2 = 289
AC = √289
AC = 17
Contoh Soal 3
Terdapat segitiga PQR siku-siku di Q. Jika diketahui panjang sisi PQ = 5cm dan QR = 12 cm, maka panjang sisi PR adalah…
Penyelesaian:
Supaya lebih mudah dalam menghitung, kita gambar terlebih dahulu segitiga siku-sikunya, seperti ini:
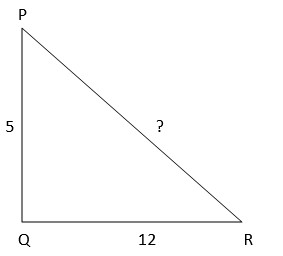
Sehingga,
PQ2 + QR2 = PR2
52 + 122 = PR2
25 + 144 = PR2
169 = PR2
PR = ±√169
PR = ±13
Karena PR itu panjang hipotenusa, yang artinya tidak boleh negatif, maka nilai PR yang memenuhi adalah 13 cm.
Contoh Soal 4
Segitiga siku-siku memiliki tinggi 9 cm dengan alas sepanjang 12 cm. Tentukanlah sisi kemiringan dari segitiga siku-siku tersebut.
Jawab:
a = 9 cm
b = 12 cm
c = ?
c2 = a2 + b2
c2 = 92 + 122
c2= 81 + 144
c= √255
c = 15
Maka sisi miringnya adalah 15 cm.
Contoh Soal 5
Sebuah segitiga ABC dengan siku-siku di A, memiliki panjang sisi miring (a) sama dengan 5 cm dan sisi mendatar (c) sama dengan 3.
1. Berapakah panjang sisi tegak (b)?
2. Berapakah keliling segitiga ABC?
Jawaban:
a kuadrat = b kuadrat + c kuadrat
5 kuadrat = b kuadrat + 3 kuadrat
25 = b kuadrat + 9
b kuadrat = 25 – 9
b = akar 16
b = 4 cm
Keliling = a + b +c
Keliling = 5 + 4 +3
Keliling = 12 cm
1. Jadi, panjang sisi tegak (b) adalah 4 cm.
2. Jadi, keliling segitiga ABC adalah 12 cm.
Contoh Soal 6
Segitiga siku-siku memiliki tinggi 9 cm dengan alas sepanjang 12 cm. Tentukanlah sisi kemiringan dari segitiga siku-siku tersebut.
Jawab:
a = 9 cm
b = 12 cm
c = ?
c2 = a2 + b2
c2 = 92 + 122
c2= 81 + 144
c= √255
c = 15
Maka sisi miringnya adalah 15 cm.
Contoh Soal 7
Sebuah segitiga siku-siku mempunyai panjang sisi miring 13 m dan panjang alasnya 5 m. Berapa keliling segitiga tersebut?
Pembahasan: Mencari tinggi dengan teorema phytagoras
c^2 = a^2 + b^2
13^2 = a^2 + 5^2
a^2 = 13^2 + 5^2
= 169 - 25
= 144
diakarkuadratkan menjadi 12
Keliling segitiga = alas + tinggi + sisi miring
= a + b + c
= 5 + 12 + 13
= 30
Contoh Soal 8
Suatu balok memiliki panjang, lebar, dan tinggi berturut-turut yaitu 12 cm, 9 cm, dan 8 cm. Tentukanlah panjang salah satu diagonal ruangnya!
Pembahasan
Diketahui:
P = 12 cm
L = 9 cm
T = 8cm
Ditanya:
Panjang dr?
Jawab:
⇒ dr2 = p2 + L2 + t2
⇒ dr2 = 122 + 9sup>2 + 82
⇒ dr2 = 144 + 81 + 64
⇒ dr2 = 289
⇒ dr = √289
⇒ dr = 17 cm
Panjang diagonal ruangnya, yaitu 17 cm.
Contoh Soal 9
2. Segitiga siku-siku KLM, jika panjang KL = 2,5 m dan KM = 6,5 m, maka keliling segitiga KLM adalah …
Penyelesaian:
Keliling segitiga KLM bisa dicari dengan menjumlahkan ketiga sisinya. Berarti, cari tahu terlebih dulu panjang sisi LM menggunakan Teorema Pythagoras.
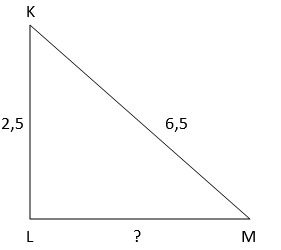
KL2 + LM2 = KM2
LM2 = KM2 – KL2
LM2 = (6,5)2 – (2,5)2
LM2 = 42,25 – 6,25
LM2 = 36
LM = ±√36
LM = ± 6
Pilih yang tandanya positif karena panjang sisi tidak mungkin negatif. Jadi, panjang sisi LM adalah 6 m. Sehingga, keliling segitiga KLM adalah,
Keliling segitiga KLM = KL + LM + KM = 2,5 + 6 + 6,5 = 15 m.
Contoh Soal 10
Suatu segitiga siku-siku memiliki sisi kemiringan sepanjang 13 cm dan alas sepanjang 12 cm. Tentukanlah berapa tinggi dari segitiga siku-siku tersebut.
Jawab:
b = 12 cm
c = 13 cm
a = ?
a2 = c2 – b2
a2 = 132 – 122
a2 = 169 – 144
a2 = 25
a = √25
a = 5
Maka tinggi dari segitiga tersebut adalah 5 cm.
Demikian ulasan lengkap mengenai rumus teorema pythagoras lengkap dengan contoh soal nya yang bisa dijadikan sebagai bahan belajar.







