Memahami Rumus Metode Cramer, Contoh Soal, dan Pembahasan
Metode cramer adalah solusi untuk menyelesaikan suatu sistem persamaan linear. Metode ini diambil dari nama penemu yaitu Gabriel Cramer (1704-1752). Gabriel Cramer adalah ahli matematika dari Swiss. Dia berkontribusi sebagai pemilah gagasan-gagasan matematis dalam sejarah matematika.
Mengutip dari Konsep-matematika.com, hasil karya Cramer terkenal yaitu Introduction a l'analyse des lignes courbes algébriques (1750). Dalam buku tersebut menjelaskan klasifikasi kurva-kurva aljabar di mana aturan Cramer membantu memperjelas aljabar matematika.
Metode Cramer
Metode Cramer digunakan untuk menyelesaikan sistem persamaan n dan persamaan dalam n variabel. Metode ini menggunakan matriks dan determinan yang perlu dipahami. Kedua metode ini menerapkan aturan cramer untuk mencari solusi sistem persamaan linear.
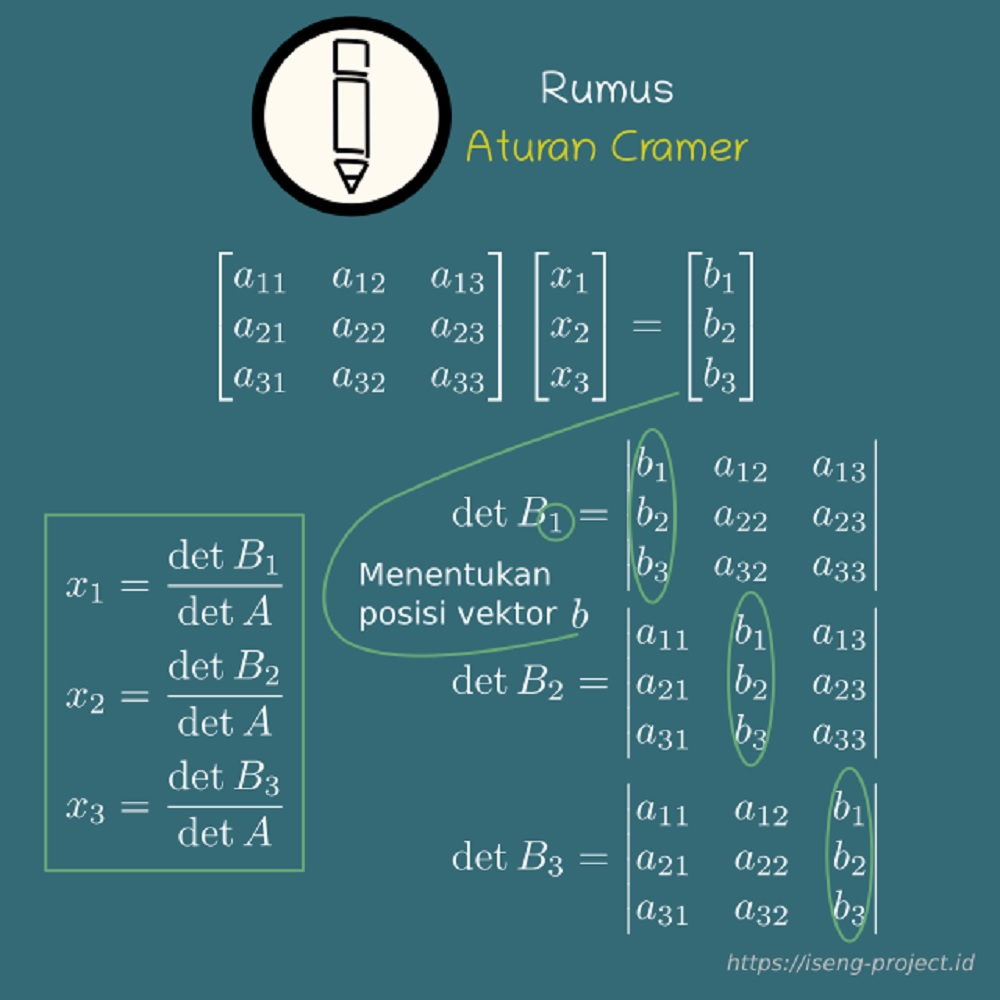
Rumus aturan Cramer dituliskan sebagai berikut:
xi = det Bi/det A
keterangan:
- Xi = Variabel yang ingin diketahui nilainya
- det B = Determinan dari matriks di mana vektor kolom ke - i diganti vektor b.
- det A = Determinan matriks A
Mengutip dari Project.id, metode cramer ini hanya mampu menyelesaikan masalah sistem persamaan. Metode Cramer berlaku jika jumlah variabel yang tidak diketahui sama dengan jumlah persamaannya. Tetapi ika banyak persamaan serta lebih sedikit menyebabkan determinan penyebutnya bernilai 0. Jika jumlah variabel lebih sedikit dapat menyebabkan matriks tidak berbentuk persegi, membuat tidak bisa dihitung determinan.
Contoh Soal Metode Cramer
Tentukan sistem persamaan linear dua variabel menggunakan sistem metode cramer.
2x - 3y = -13
x + 2y = 4
Penyelesaian sistem persamaan linear dua variabel (SPDLV) dinyatakan dalam bentuk matriks.
Jadi nilai x dan y yang memenuhi SPLDV di atas yaitu x = -2 dan y = 3
Kelebihan dan Kekurangan Metode Cramer
Penggunaan metode cramer tidak perlu repot menggali faktor pengali yang dibutuhkan untuk eliminasi. Tidak perlu menyusun ulang baris matriksnya, jika pivot bernilai nol. Metode cramer bisa langsung dipakai rumus secara mentah-mentah. Tetapi, jika determinan A nol maka dianggap tidak ada solusi, meski belum tentu. Nilai determinan menentukan apakah matriksnya dapat di invers atau tidak. Sehingga ada pengaruh Ax = b.