Mencermati Rumus Peluang Kombinasi Beserta Contoh Soalnya

Dalam ilmu matematika, peluang merupakan materi yang membahas tentang kemungkinan munculnya suatu kejadian. Dalam materi ini, terdapat beberapa istilah yang perlu dipelajari.
Salah satunya yaitu peluang kombinasi. Dikutip dari Cue Math, kombinasi adalah pilihan yang dibuat dengan mengambil sebagian atau seluruh objek terlepas dari aturannya.
Oleh karena itu, bisa dikatakan bahwa peluang kombinasi merupakan cara menyusun atau mengambil objek tanpa memperhatikan urutan.
Peluang kombinasi biasanya diterapkan ketika menentukan pemilihan tim atau kelompok, baju, mata pelajaran, dan makanan. Materi ini juga dapat diterapkan dalam perlombaan untuk mengambil 3 pemenang secara acak.
Namun dalam menentukan hal ini, terdapat rumus peluang kombinasi yang harus digunakan. Untuk lebih detailnya, simak ulasannya berikut ini.
Rumus Peluang Kombinasi
Dalam menghitung peluang kombinasi, terdapat rumus yang digunakan yaitu
C(n, r) = n!/(r! (n – r)!)
Keterangan:
C(n, r) : permutasi r objek dari n objek yang ada
n : banyaknya objek keseluruhan
r : banyaknya objek yang diamati/diberi perlakuan
Contoh Soal
Berikut ini 10 contoh soal peluang kombinasi yang bisa dipelajari agar lebih paham tentang materi ini.
Contoh Soal 1
Terdapat himpunan huruf A,B,C,D. Akan dihitung susunan dengan dua huruf tanpa berurutan. Ada berapa banyak susunan dua huruf tersebut?
Dari contoh di atas, Anda bisa menggabungkan dengan manual menjadi AB, AC, AD, BC, BD, CD. Namun jika menggunakan rumus, artinya dengan n = 4 dan r=2 maka
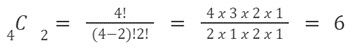
Penyelesaian contoh soal kombinasi 1. Foto: Cue Math
Contoh Soal 2
Di suatu ujian, setiap siswa harus menjawab 4 dari 7 soal yang ada. Jika seorang siswa secara acak memilih soal untuk dikerjakan, berapa banyak cara atau pilihan soal yang bisa dikerjakan siswa itu?
Dengan n = 7 dan r = 4 maka,
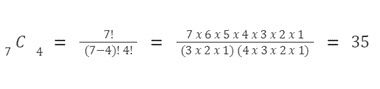
Penyelesaian contoh soal kombinasi 2. Foto: Cue Math
Contoh Soal 3
Dari 4 bus di terminal akan dipilih 2 bus untuk berangkat ke Yogyakarta. Berapakah cara memilih bus tersebut?
Pembahasan:
4C2 = 4! / (2! (4-2)!)
4C2 = (4×3×2×1) /((2×1)(2×1))
4C2 = (4×3) /(2×1))
4C2 = 12 / 2 = 6
Jadi, banyaknya cara untuk memilih bus yang berangkat ke Yogyakarta adalah 6 cara.
Contoh Soal 4
Rudi pergi ke kamar untuk mengambil 3 jenis buku. Jika di kamarnya terdapat 6 jenis buku, hitung banyaknya kombinasi tiga jenis buku yang mungkin dibawa oleh Rudi ?
Pembahasan:
6C3 = 6!/(3!(6-3)!)
6C3 = (6×5×4×3×2×1) / ((3×2×1)(3×2×1))
6C3 = (6×5×4) / (3×2×1)
6C3 = 5×4 = 20
Jadi, kombinasi tiga jenis buku yang mungkin dibawa oleh Rudi adalah 20 kombinasi.
Contoh Soal 5
Pada suatu arisan yang dihadiri 7 ibu. Ke tujuh ibu tersebut saling berjabat tangan satu sama lain. Hitunglah banyak jabat tangan yang terjadi?
Pembahasan:
7C2 = 7!/(2!(7-2)!)
7C2 = 7!/(2! 5!)
7C2 = (7×6×5×4×3×2×1) / ((2×1)(5×4×3×2×1))
7C2 = (7×6) / 2
7C2 = 21
Jadi, banyaknya jabat tangan yang terjadi adalah 21 jabat tangan.
Contoh Soal 6
Kepengurus RT terdiri dari 5 orang laki-laki dan 3 orang wanita akan dipilih 4 perwakilan untuk menghadiri upacara 17 Agustus. Hitung banyak cara memilih jika perwakilan terdiri dari 2 orang laki-laki dan 2 orang perempuan?
Pembahasan
Cara memilih 2 laki-laki:
5C2 = 5!/(2!(5-2)!)
5C2 = 5!/(2! 3!)
5C2 = (5×4×3×2×1) / ((2×1)(3×2×1))
5C2 = (5×4) / 2
5C2 = 10
Cara memilih 2 perempuan
3C2 = 3!/(2!(3-2)!)
3C2 = 3!/ 2!
3C2 = (3×2×1) / (2×1)
3C2 = 3
Cara memilih 2 laki-laki dan 2 perempuan = 10 × 3 = 30
Jadi, banyaknya cara memilih perwakilan RT tersebut adalah 30 cara.
Contoh Soal 7
Tia ingin membeli 6 jenis boneka di toko yang menjual 9 jenis boneka. Jika 2 jenis boneka sudah pasti dibeli, berapa banyak kombinasi 6 boneka yang mungkin dibeli Tia?
Pembahasan:
Karena 2 jenis boneka sudah pasti dibeli, Tia tinggal memilih sisanya, yaitu 6-2 = 4 jenis boneka dari sisa jenis boneka yang belum dipilih, yaitu 9-2 =7, maka:
7C4 = 7!/(4!(7-4)!)
7C4 = 7!/ (4!3!)
7C4 = (7×6×5×4×3×2×1) / ((4×3×2×1)(3×2×1))
7C4 = (7×6×5) / (3×2×1)
7C4 = 7×5
7C4 = 35
Jadi, kombinasi 6 boneka yang mungkin dibeli Tia ada 35.
Contoh Soal 8
Pada sebuah box terdapat 10 kelereng kecil yang sudah diberi tulisan huruf A hingga J. Seorang anak ingin mengambil 4 sekaligus secara acak. Ada berapa cara yang bisa ia gunakan untuk mengambilnya?
Pembahasan:
C (n,r) = n! / r! . (n – r)!
C (10,4) = 10! / 4! . (10 – 4)!
= 10 x 9 x 8 x 7 x 6! / 4 x 3 x 2 x 1 x 6!
= 5 x 3 x 2 x 7 x 6! / 6!
= 5 x 3 x 2 x 7
= 210
Contoh Soal 9
Seorang dosen ingin meminta bantuan pada 5 mahasiswanya. Di mata kuliah yang ia pegang, jumlah mahasiswa totalnya sebanyak 20. Ada berapa cara yang dapat digunakan untuk memilih kelima mahasiswa tersebut?
Pembahasan:
C (n,r) = n! / r! . (n – r)!
C (20,5)= 20! / 5!. (20 – 5)!
= 20 x 19 x 18 x 17 x 16 x 15! / 5 x 4 x 3 x 2 x 1 x 15!
= 4 x 19 x 6 x 17 x 4 x 15! / 2 x 15!
= 2 x 19 x 6 x 17 x 4
= 15.504
Contoh Soal 10
Pada suatu jenis seleksi masuk Perguruan Tinggi, hanya ada 15 kampus yang diizinkan mengadakan seleksi bersamaan.
Setiap pendaftar pun hanya diizinkan mendaftar 3 kampus dari 15 kampus yang ditawarkan. Ada berapa cara pemilihan kampus yang bisa dilakukan oleh mahasiswa agar sesuai syarat?
Pembahasan:
C (n,r) = n! / r! . (n – r)!
C (15,3) = 15! / 3! . (15 – 3)!
= 15 x 14 x 13 x 12! / 3 x 2 x 1 x 12!
= 5 x 7 x 13 x 12! / 12!
= 5 x 7 x 13
= 455







