Mencermati Rumus dan Contoh Soal Teorema Pythagoras sebagai Bahan Belajar
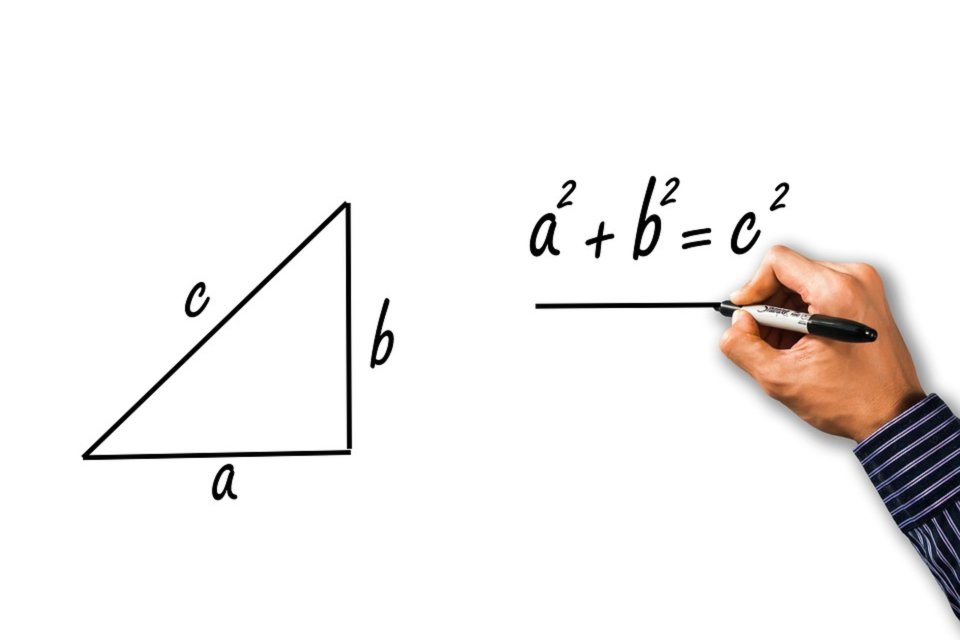
Teorema pythagoras merupakan salah satu materi matematika yang dipelajari saat SMP, tepatnya kelas 8.
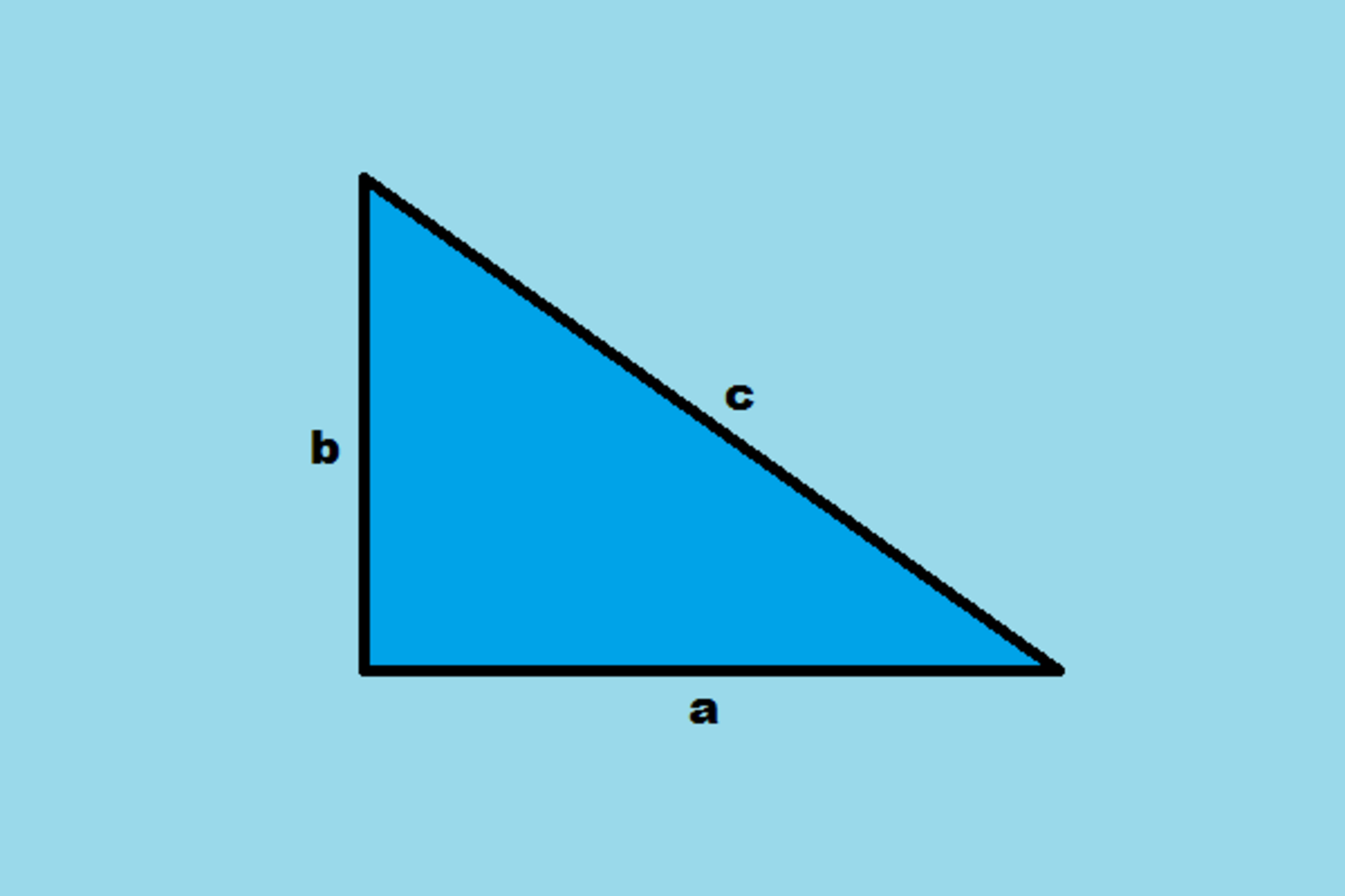
Dilansir dari buku Matematika: Belajar Ringkas Matematika yang Mudah dan Menyenangkan, Ayubkasi Soromi, Solikrisman Laia, dan Darmawan Harefa (2020:104), teorema pythagoras adalah teorema yang menunjukkan hubungan antarsisi pada segitiga siku-siku.
Di mana dalam materi ini, kuadrat sisi miring segitiga siku-siku adalah jumlah kuadrat kedua sisi lainnya.
Untuk lebih memahami materi ini, berikut di bawah ini ulasan lengkapnya, mulai dari rumus hingga contoh soal teorema pythagoras yang bisa dipelajari.
Rumus Teorema Pythagoras
Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi yang pendek (kaki tegak dan kaki samping).
Mengutip dari buku Rumus Lengkap Matematika SMP karya Drs. Joko Untoro, berikut rumus phytagoras:
Dalam bentuk matematis, rumus pythagoras dapat ditulis sebagai:
c² = a² + b²
di mana c adalah panjang hipotenusa, dan a dan b adalah panjang kedua sisi yang pendek
Rumus diatas digunakan untuk mencari sisi miring atau sisi terpanjang pada segitiga siku-siku.
Untuk mencari sisi depan dan sisi sampingnya, rumus yang digunakan, yaitu:
a² = c² - b² (untuk mencari sisi depan)
b² = c² - a² (untuk mencari sisi samping)
Perlu diingat, dalam menentukan persamaan phytagoras, perlu diperhatikan siapa yang berkedudukan sebagai sisi miring dari segitiga siku-siku. Selain itu, akan lebih cepat juga untuk mencari sisi yang ditanya jika menghafalkan triple pythagoras.
Berikut ini beberapa pola dari triple phytagoras:
- 3, 4, 5
- 5, 12, 13
- 6, 8, 10
- 7, 24, 25
- 8, 15, 17
- 9, 40, 41
- 11, 60, 61
- 12, 35, 37
- 13, 84, 85
- 13, 84, 85
Contoh Soal Teorema Pythagoras
Agar lebih mudah memahami materi teorema pythagoras, berikut ini sepuluh contoh soal dan pembahasannya yang telah dirangkum dari berbagai sumber.
Contoh Soal 1
Sebidang tanah berbentuk segitiga siku-siku, panjang sisi miringnya 35 m dan panjang alasnya 21 m. Berapa tinggi dari segitiga tersebut?
Pembahasan: Mencari tinggi dengan teorema phytagoras
c^2 = a^2 + b^2
35^2 = a^2 + 21^2
a^2 = 35^2 - 21^2
= 1.225 - 441
= 784 diakarkuadratkan menjadi 28
Kunci jawaban:. 28
Contoh Soal 2
Sebuah bangun berbentuk segitiga siku-siku, panjang sisi miringnya 10 m dan panjang alasnya 8 m. Berapa luas bangun tersebut?
Pembahasan: Mencari tinggi dengan teorema phytagoras
c^2 = a^2 + b^2
10^2 = a^2 + 8^2
a^2 = 10^2 + 8^2
= 100 - 64
= 36 diakarkuadratkan menjadi 6
Luas segitiga = alas x tinggi : 2
= 8 x 6 : 2
= 48 : 2
= b. 24
Kunci jawaban: 24
Contoh Soal 3
Sebuah segitiga siku-siku mempunyai panjang sisi miring 13 m dan panjang alasnya 5 m. Berapa keliling segitiga tersebut?
Pembahasan: Mencari tinggi dengan teorema phytagoras
c^2 = a^2 + b^2
13^2 = a^2 + 5^2
a^2 = 13^2 + 5^2
= 169 - 25
= 144 diakarkuadratkan menjadi 12
Keliling segitiga = alas + tinggi + sisi miring
= a + b + c
= 5 + 12 + 13
= c. 30
Kunci jawaban: 30
Contoh Soal 4
Segitiga siku-siku memiliki tinggi 9 cm dengan alas sepanjang 12 cm. Tentukanlah sisi kemiringan dari segitiga siku-siku tersebut.
Jawab:
a = 9 cm
b = 12 cm
c = ?
c2 = a2 + b2
c2 = 92 + 122
c2= 81 + 144
c= √255
c = 15
Maka sisi miringnya adalah 15 cm.
Contoh Soal 5
Suatu segitiga siku-siku memiliki sisi kemiringan sepanjang 13 cm dan alas sepanjang 12 cm. Tentukanlah berapa tinggi dari segitiga siku-siku tersebut.
Jawab:
b = 12 cm
c = 13 cm
a = ?
a2 = c2 – b2
a2 = 132 – 122
a2 = 169 – 144
a2 = 25
a = √25
a = 5
Maka tinggi dari segitiga tersebut adalah 5 cm.
Contoh Soal 6
Tentukan jenis segitiga yang memiliki panjang sisi 5 cm, 7 cm dan 8 cm?
Jawab:
Sisi terpanjang adalah 8 cm, maka:
a = 8 cm, b = 7 cm, c = 5 cm
a² = 82 = 64
b²+ c² = 72 + 52
b²+ c² = 49 + 25
b²+ c² = 74
Dikarenakan a² < b²+ c² , maka dapat disimpulkan bahwa segitiga tersebut adalah segitiga lancip.
Contoh Soal 7
Sisi yang dimaksud merupakan sisi miring segitiga siku-siku (hipotenusa).
Sehingga:
c2 = a2 + b2
= 212 + 282 = 441 + 784 = 1.225
c = √1.225 = 35 cm
Cara cepat:
Dengan menggunakan tripel (3, 4, 5) maka setiap sisi segitiga dikali dengan 7 sehingga
(3 x 7, 4 x 7, 5x 7) sehingga (21, 28, 35)
Panjang sisi yang lain adalah 35 cm.
Contoh Soal 8
Untuk mencari nilai x dapat mempergunakan Teorema Pythagoras yakni:
BC2 = AC2 + AB2
(2x + 2)2 = 42 + (2x + 1)2
4x2 + 8x + 4 = 16 + 4x2 + 4x + 1
4x2 + 8x + 4 = 4x2 + 4x + 17
4x = 13
x = 13/4
x = 3,25
Jadi nilai x yang memenuhi adalah 3,25
Panjang sisi miring merupakan panjang BC, maka:
BC = (2x + 2) cm
BC = (2 . 3,25 + 2) cm
BC = (6,5 + 2) cm
BC = 8,5 cm
Jadi, panjang sisi miringnya adalah 8,5 cm
Contoh Soal 9
Segitiga siku-siku memiliki sisi hipotenusa 10 cm dan tinggi 6 cm. Berapakah panjang dari alas segitiga siku-siku tersebut.
Jawab:
a = 6 cmc = 10 cm
b = ?
b2 = c2 – a2
b2 = 102 – 62
b2 = 100 – 36
b2 = 64
b = √64
b = 8
Maka panjang dari alas segitiga siku-siku tersebut adalah 8 cm.
Contoh Soal 10
Pak Budi berencana untuk membuat wahana perosotan untuk anaknya dengan menggunakan peralatan yang ada di rumahnya. Jika jarak tempat tujuan akhir perosotan dengan tempat untuk naik yang tersedia di rumah adalah 8 meter dan tinggi dari tempat naik atau tangga dari perosotan itu adalah 6 meter, berapakah panjang sisi miring tempat untuk perosotan itu?
Jawab
Jika digambarkan dalam bentuk segitiga siku-siku maka bentuk dari flying fox itu adalah seperti ini:
Maka dapat diartikan bahwa tangga naik sama dengan tinggi segitiga, yaitu 6 cm dan jarak sama dengan alas, yaitu 8 cm.
a = 6 cm
b = 8 cm
c = ?
c
2 = a2 + b2
c2 = 62 + 82
c2= 36 + 64
c= √100
c = 10
Maka panjang dari sisi miring perosotan itu adalah 10 m.
Demikian ulasan lengkap mengenai rumus dan contoh soal teorema pythagoras lengkap dengan pembahasannya yang bisa dijadikan sebagai bahan belajar.