15 Contoh Soal UTBK SNBT 2025 Penalaran Matematika Beserta Pembahasannya

Pada tahun ini, pelaksanaan Ujian Tulis Berbasis Komputer (UTBK) Seleksi Nasional Berdasarkan Tes (SNBT) 2025 akan dilaksanakan mulai 23 April hingga 3 Mei 2025.

UTBK SNBT merupakan tahapan penting bagi calon mahasiswa untuk masuk ke perguruan tinggi impian.

Umumnya, terdapat empat materi pelajaran yang akan masuk dalam ujian. Salah satunya penalaran matematika, yang berisi beragam soal untuk menguji kemampuan calon mahasiswa menerapkan matematika dasar dalam memecahkan masalah di kehidupan sehari-hari. 

Mengingat pentingnya tes ini, calon mahasiswa diimbau untuk mempersiapkan diri dengan mempelajari contoh soal UTBK SNBT 2025 lengkap dengan pembahasannya.

Berikut di bawah ini kumpulan contoh soal UTBK SNBT 2025 penalaran matematika dan pembahasannya sebagai bahan latihan.

Contoh Soal UTBK SNBT 2025 Penalaran Matematika

Dikutip dari berbagai sumber, berikut ini 15 contoh soal UTBK SNBT 2025 untuk materi penalaran matematika lengkap dengan pembahasannya yang bisa dijadikan sebagai bahan belajar.

Contoh Soal UTBK SNBT 2025 Penalaran Matematika (Pexels)

1. Topik: Bilangan

Subtopik: Konsep Kilat Operasi Hitung Bilangan

Perhatikan ilustrasi berikut!

Anggun membawa tiga buah barang, yaitu A, B, dan C yang beratnya berturut-turut 1.450 g, 0,5 kg, dan 3,2 kg ke WahAda Cargo untuk dikirimkan ke Cimahi. Berikut ini tabel yang menunjukkan biaya pengiriman barang.

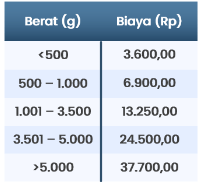
Apabila terdapat potongan harga sebesar 10% untuk setiap pengiriman barang, total biaya yang dikeluarkan Anggun untuk mengirimkan barang A, B, dan C secara terpisah adalah ….

1. Rp28.060,00
2. Rp30.060,00
3. Rp33.400,00
4. Rp35.490,00
5. Rp37.700,00

Jawaban: B

Pembahasan:

Diketahui bahwa barang A seberat 1.450 g barang B seberat 0,5 kg = 500 g dan barang C seberat 3,2 g = 3.200 g.

Total biaya yang dikeluarkan untuk mengirimkan barang A, B, dan C secara terpisah dapat dihitung sebagai berikut.

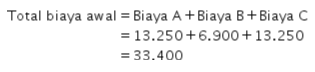
Karena setiap pengiriman barang akan mendapatkan potongan harga sebesar , maka biaya yang dikeluarkan Anggun menjadi sebagai berikut.

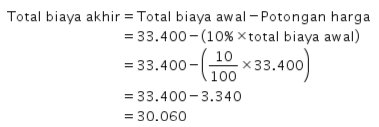
Dengan demikian, total biaya yang dikeluarkan Anggun untuk mengirimkan barang A, B, dan C secara terpisah adalah Rp30.060,00.

2.  Subtopik : Kemampuan Nalar pada Bilangan

Level Kognitif : HOTS

Perhatikan teks berikut!

Di sebuah peternakan ayam petelur, ayam-ayam yang diternak dibagi ke dalam 3 kelompok berbeda. Telur-telur dari ayam pada kelompok 1, 2, dan 3 secara berurutan dikumpulkan setiap 3 hari sekali, 4 hari sekali, dan 6 hari sekali. Dalam sekali pengambilan, rata-rata banyak telur yang dapat dikumpulkan dari ayam pada kelompok 1, 2, dan 3 secara berurutan adalah 100 butir telur, 150 butir telur, dan 225 butir telur.

Dalam 12 hari, perkiraan banyak telur yang dapat dikumpulkan dari ayam pada ketiga kelompok adalah … butir telur.

1. 2.250
2. 1.300
3. 950
4. 825
5. 475

Kunci Jawaban : B

Pembahasan :

Langkah pertama: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 1 dalam 12 hari.

Telur ayam pada kelompok 1 diambil setiap 3 hari sekali dan rata-rata dapat dikumpulkan 100 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 1 diambil sebanyak  kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 100 × 4 = 400 butir telur.

Langkah kedua: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 2 dalam 12 hari.

Telur ayam pada kelompok 2 diambil setiap 4 hari sekali dan rata-rata dapat dikumpulkan 150 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 2 diambil sebanyak  kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 150 × 3 = 450 butir telur.

Langkah ketiga: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 3 dalam 12 hari.

Telur ayam pada kelompok 3 diambil setiap 6 hari sekali dan rata-rata dapat dikumpulkan 225 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 3 diambil sebanyak  kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 225 × 2 = 450 butir telur.

Langkah keempat: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada ketiga kelompok dalam 12 hari.

Dalam 12 hari, perkiraan banyak telur yang dapat dikumpulkan dari kelompok 1, 2, dan 3 secara berurutan adalah 400, 450, dan 450 butir telur. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan dari ayam pada ketiga kelompok dalam 12 hari adalah 400 + 450 + 450 = 1. 300 butir telur.

Analisis pilihan jawaban yang salah

• Pilihan jawaban A, yaitu 2.250, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan terjadi saat menghitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada masing-masing kelompok yang seharusnya mengalikan banyak telur yang dikumpulkan dalam sekali pengumpulan dengan banyak pengambilan, tetapi justru mengalikan banyak telur yang dikumpulkan dalam sekali pengumpulan dengan durasi jeda antar pengambilan telur, yaitu 100 × 3 + 150 × 4 + 225 × 6 = 2. 250.
• Pilihan jawaban C, yaitu 950, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah menganggap bahwa telur diambil sebanyak 2 kali saja (didapat dari 12 hari yang dibagi dengan jeda waktu terlama antar pengambilan telur, yaitu 6 hari). Oleh karena itu, perhitungannya justru menjadi 2 × (100 + 150 + 225) = 950.
• Pilihan jawaban D, yaitu 825, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah dengan menganggap tidak ada pengambilan telur di hari ke-12 sehingga banyak pengambilan telur dari masing-masing kelompok berkurang 1. Banyak pengambilan telur di kelompok 1 menjadi 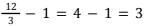 kali, banyak pengambilan telur di kelompok 2 menjadi  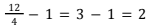kali, dan banyak pengambilan telur di kelompok 3 menjadi  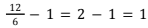kali. Oleh karena itu, perhitungannya justru menjadi 100 × 3 + 150 × 2 + 225 × 1 = 825.
• Pilihan jawaban E, yaitu 475, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah menganggap bahwa telur diambil sebanyak 1 kali saja. Oleh karena itu, perhitungannya justru menjadi 100 + 150 + 225 = 475.

Jadi, jawaban yang tepat adalah B.

3. Subtopik : Kemampuan Nalar pada Bilangan

Level Kognitif : HOTS

Perhatikan ilustrasi berikut!

Lantai sebuah aula yang berbentuk persegi akan dipasang keramik berwarna putih dan keramik berwarna hitam dengan pola sebagai berikut.

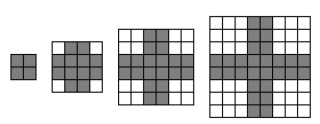
Jika perbandingan banyak keramik putih dan hitam adalah 81: 19, total banyak keramik (hitam dan putih) di aula tersebut adalah … ubin keramik.

Catatan: Tidak ada keramik yang dipotong

1. 100
2. 200
3. 400
4. 500
5. 600

Kunci Jawaban : C

Pembahasan :

Diketahui lantai aula berbentuk persegi yang akan dipasangi keramik-keramik berwarna putih dan hitam. Berdasarkan gambar, pola pertama memiliki dimensi ukuran 2 × 2, pola kedua 4 × 4, dan seterusnya.

Berdasarkan informasi pada soal, dapat diperhatikan bahwa untuk aula berdimensi n × n, banyak keramik putih akan mengikuti rumus berikut.

Jika banyak keramik putih adalah , maka banyak keramik hitamnya adalah total keramik dikurang banyak keramik putih, yakni

Diketahui perbandingan banyak keramik putih dan hitam 81: 19. Akibatnya, akan diperoleh perhitungan berikut.

Diperoleh , tetapi karena n menyatakan banyaknya keramik, maka nilai n harus bernilai bulat. Oleh karena itu, diperoleh nilai n yang memenuhi adalah n = 20.

Dengan demikian, total banyak keramik (hitam dan putih) di aula tersebut adalah 

Jadi, jawaban yang tepat adalah C.

4. Perhatikan informasi berikut ini!

Sampah anorganik lebih lama terurai dibandingakn dengan sampah organik. Waktu dekomposisi popok sekali pakai lebih lama dari plastik, namun kurang dari kulit sintetis. Berapa waktu dekomposisi yang mungkin dari popok sekali pakai?

1. 100 tahun
2. 250 tahun
3. 375 tahun
4. 475 tahun
5. 575 tahun

Jawaban: D

Pembahasan:

Kunci dalam mengerjakan soal ini adalah fokus ke pertanyaannya.

Pertanyaannya adalah berapa waktu dekomposisi dari popok sekali pakai? Maka, kita bisa langsung fokus ke popok sekali pakai dengan melihat informasi tambahan yang tersedia. Nah, dari informasi yang tersedia, kita bisa tahu bahwa waktu dekomposisi popok sekali pakai, lebih lama dibandingkan plastik (lebih dari 400 tahun), tetapi lebih sebentar dari kulit sintetis (kurang dari 500 tahun).

Nah, dari informasi tersebut, jawaban yang paling tepat adalah dekomposisi popok sekali pakai memakan waktu hingga 475 tahun.

Maka, jawaban yang benar adalah D.

5. Pajak Penghasilan (PPh) berdasarkan UU PPh didefinisikan sebagai pajak yang dikenakan kepada orang pribadi atau badan atas penghasilan yang diperoleh dalam tahun pajak. Untuk Penghasilan Tidak Kena Pajak (PTKP), karyawan yang memiliki status belum menikah dan tidak memiliki tanggungan adalah Rp54.000.000,00 per tahun. PPh termasuk ke dalam pajak progresif sehingga tarif pajak yang akan makin naik sesuai dengan naiknya dasar pengenaan pajak. Diketahui perhitungan tarif PPh berdasarkan pasal 21 sesuai UU PPh didasari oleh Penghasilan Kena Pajak (PKP) dan disajikan dalam tabel berikut.

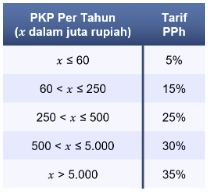
Sebagai contoh, untuk penghasilan Andi setelah dikurangi PTKP adalah Rp300.000.000,00 per tahun, maka dikenakan tarif pajak sampai lapis ketiga, yaitu 25%. Pada tarif lapis pertama, Rp60.000.000,00 pertama dikenakan tarif pajak 5%. Kemudian, pada tarif lapis kedua, Rp190.000.000,00 berikutnya (dari 60 juta sampai 250 juta) dikenakan tarif pajak 15%. Selanjutnya, pada tarif lapis terakhir, sisa Rp50.000,000 dikenakan tarif pajak 25%.

Nisa adalah seorang karyawan tetap di suatu perusahaan dengan status belum menikah dan tidak memiliki tanggungan dengan penghasilan netto sebesar Rp42.500.000,00 per bulan. Persentase tarif PPh progresif yang dikenakan kepada Nisa adalah sampai ….

1. 5%
2. 15%
3. 25%
4. 30%
5. 35%

Jawaban: C

Pembahasan:

Misalkan penghasilan Nisa selama 1 tahun adalah P, maka besarnya dalam setahun yaitu sebagai berikut.

P = Rp 42.500.000,00 x 12

P = Rp 510.000.000,00

Misalkan penghasilan kena pajak Nisa sebesar , maka karena Nisa belum menikah dan tidak memiliki tanggungan, PTKPnya sebesar Rp54.000.000,00, sehingga besarnya penghasilan Nisa yang kena pajak yaitu sebagai berikut.

 = P – 54.000.000,00

 = 510.000.000, 00 – 54.000.000,00

 = 456.000.000,00

Dengan membandingkan  dengan tabel yang diberikan dalam soal, maka penghasilan kena pajak Nisa akan dikenakan tarif progresif sebesar 25%.

Jadi, jawaban yang benar adalah C.

6. Topik: Perbandingan Jumlah Siswa

Perhatikan ilustrasi berikut!

Kelompok Belajar

Suatu kelompok belajar terdiri dari siswa laki-laki dan siswa perempuan. Salah satu siswa laki-laki bernama Edo dan salah satu siswa perempuan bernama Tari. Banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki.

Jika siswa laki-laki bertambah 1 dan siswa perempuan berkurang 1, perbandingan banyak siswa laki-laki dan perempuan di kelompok tersebut adalah ….

1. 1:1
2. 1:2
3. 2:1
4. 2:3
5. 3:4

Jawaban: A

Pembahasan:

Misalkan banyak siswa laki-laki di kelompok tersebut adalah x dan banyak siswa perempuan di kelompok tersebut adalah y.

Diketahui banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Artinya, dapat dibuat persamaan berikut.

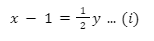
Kemudian, diketahui banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki. Artinya, dapat dibuat persamaan berikut.

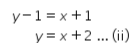
Substitusikan persamaan ii ke persamaan i sehingga didapat nilai x sebagai berikut.

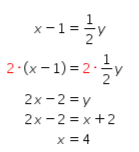
Substitusikan nilai x = 4 ke persamaan ii sehingga didapat nilai y sebagai berikut.

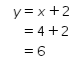
Didapat bahwa banyak siswa laki-laki dan perempuan di kelompok belajar tersebut secara berurutan adalah 4 dan 6.

• Jika siswa laki-laki bertambah 1, banyak siswa laki-laki menjadi 4 + 1 = 5 siswa.
• Jika siswa perempuan berkurang 1, banyak siswa perempuan menjadi 6 – 1 = 5 siswa.

Dengan demikian, perbandingan banyak siswa laki-laki dan perempuan di kelompok tersebut adalah 5:5 = 1:1.

Jadi, jawaban yang tepat adalah A.

7. Topik: Peluang

Perhatikan ilustrasi berikut!

Kelompok Belajar

Suatu kelompok belajar terdiri dari siswa laki-laki dan siswa perempuan. Salah satu siswa laki-laki bernama Edo dan salah satu siswa perempuan bernama Tari. Banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki.

Banyak cara memilih 2 orang siswa jika setidaknya terpilih 1 orang siswa laki-laki adalah ….

1. 6
2. 12
3. 24
4. 30
5. 36 

Jawaban: D

Pembahasan:

Misalkan banyak siswa laki-laki di kelompok tersebut adalah x dan banyak siswa perempuan di kelompok tersebut adalah y.

Diketahui banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Artinya, dapat dibuat persamaan berikut.

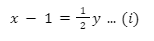
Kemudian, diketahui banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki. Artinya, dapat dibuat persamaan berikut.

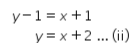
Substitusikan persamaan ii ke persamaan i sehingga didapat nilai x sebagai berikut.

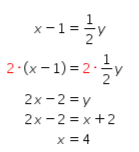
Substitusikan nilai x = 4 ke persamaan ii sehingga didapat nilai y sebagai berikut.

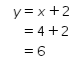
Didapat bahwa banyak siswa laki-laki dan perempuan di kelompok belajar tersebut secara berurutan adalah 4 dan 6.

Selanjutnya, akan dipilih 2 orang siswa dengan syarat terpilih setidaknya 1 orang siswa laki-laki. Dalam hal ini, akan terdapat dua kasus sebagai berikut.

Kasus 1: Terpilih 1 siswa laki-laki dan 1 siswa perempuan.

Banyak cara memilih 2 orang siswa pada kasus ini dapat dihitung sebagai berikut.

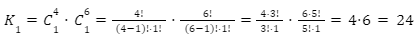
Kasus 2: Terpilih 2 siswa laki-laki.

Banyak cara memilih 2 orang siswa pada kasus ini dapat dihitung sebagai berikut.

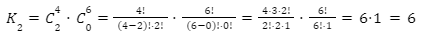
Perhatikan bahwa kejadian memilih siswa pada kasus 1 dan kasus 2 tidak mungkin terjadi secara bersamaan. Artinya, kejadian memilih siswa ini merupakan kejadian saling lepas. Oleh karena itu, total banyak cara memilih 2 orang siswa tersebut dapat dihitung menggunakan aturan penjumlahan, yaitu 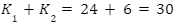 cara.

Jadi, jawaban yang tepat adalah D.

8. Topik: Pendapatan Maksimum

Perhatikan ilustrasi berikut!

Bianglala

Sebuah bianglala di taman hiburan memiliki 36 kabin penumpang. Setiap kabin hanya boleh diisi oleh 2 orang dewasa atau 1 orang dewasa dan 2 anak-anak. Berikut adalah daftar harga tiket bianglala tersebut.

• Senin–Jumat: anak-anak Rp20.000,00 dan dewasa Rp30.000,00
• Sabtu, Minggu, dan Hari libur: anak-anak Rp35.000,00 dan dewasa Rp50.000,00

Jika pada jam 18.30 di hari Minggu setengah kabin diisi oleh anak-anak dan seluruh kabin tidak ada yang kosong, jumlah pendapatan maksimum taman hiburan dari bianglala yang mungkin diperoleh pada saat itu adalah ….

1. Rp1.260.000,00
2. Rp2.340.000,00
3. Rp2.700.000,00
4. Rp2.610.000,00
5. Rp3.960.000,00

Jawaban: E

Pembahasan:

Berdasarkan informasi pada soal, disebutkan bahwa kondisinya adalah sebagai berikut.

Hari Minggu, maka harga tiket anak-anak Rp35.000,00 dan dewasa Rp50.000,00.

Setengah kabin (18 kabin) diisi anak-anak = tidak boleh ada kabin yang hanya diisi anak-anak, maka harus ada orang dewasa. Karena yang ditanyakan adalah pendapatan maksimum, maka digunakan asumsi sejumlah 18 kabin diisi 1 dewasa dan 2 anak-anak.

Seluruh kabin tidak ada yang kosong, maka 18 kabin sisanya diisi oleh 2 orang dewasa.

Pendapatan maksimum yang mungkin diperoleh dapat diketahui dengan perhitungan berikut

Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa jumlah pendapatan maksimum taman hiburan dari bianglala yang mungkin diperoleh pada saat itu adalah Rp3.960.000,00.

Jadi, jawaban yang tepat adalah E.

Contoh Soal UTBK SNBT 2025 Penalaran Matematika (Pexels)

9. Topik: Menghitung Jumlah dalam Suatu Rentang Waktu

Perhatikan teks berikut!

Data Covid-19 Tahun 2022

Per 1 September 2020, Indonesia telah melaporkan 177.571 kasus positif COVID-19, dengan catatan sebanyak 42.009 dirawat/isolasi mandiri, 128.057 sembuh, dan 7.505 meninggal. Case fatality ratio (CFR) adalah proporsi individu terkonfirmasi penyakit yang meninggal karena penyakit tersebut. Berikut merupakan data perkembangan kasus pasien COVID-19.

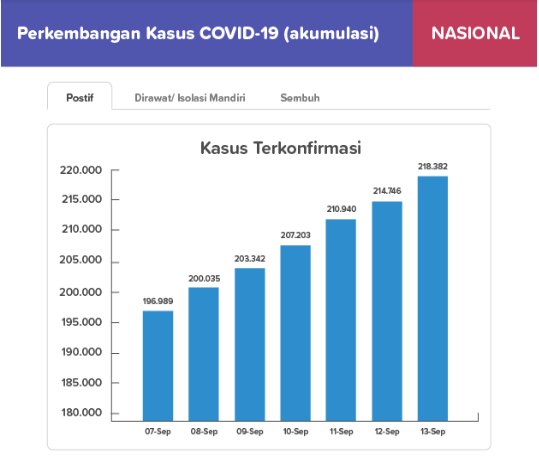
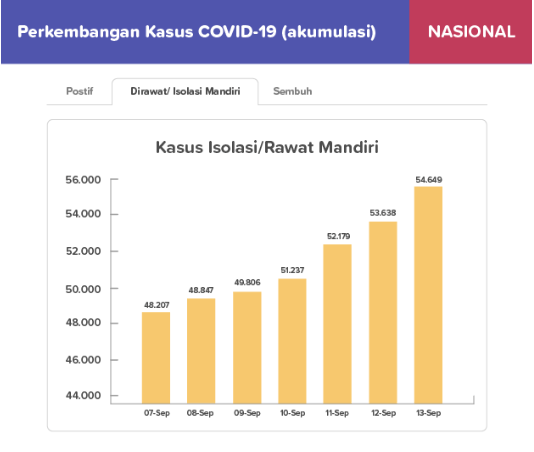
Penambahan kasus terkonfirmasi tertinggi terjadi pada rentang tanggal ….

1. 7 September – 8 September
2. 9 September – 10 September
3. 10 September – 11 September
4. 11 September – 12 September
5. 12 September – 13 September

Jawaban: B

Pembahasan: 

Berdasarkan informasi pada soal dapat diketahui jumlah kasus terkonfirmasi adalah sebagai berikut.

• 7 September 2020 = 196.989
• 8 September 2020 = 200.035
• 9 September 2020 = 203.342
• 10 September 2020 = 207.203
• 11 September 2020 = 210.940
• 12 September 2020 = 214.746
• 13 September 2020 = 218.382

Penambahan kasus terkonfirmasi pada rentang tanggal 7 September – 8 September

= 200.035 – 196.989 = 3.046

Penambahan kasus terkonfirmasi pada rentang tanggal 9 September – 10 September

= 207.203 – 203.342 = 3.861

Penambahan kasus terkonfirmasi pada rentang tanggal 10 September – 11 September

= 210.940 – 207.203 = 3.737

Penambahan kasus terkonfirmasi pada rentang tanggal 11 September – 12 September

= 214.746 – 210.940 = 3.806

Penambahan kasus terkonfirmasi pada rentang tanggal 12 September – 13 September

= 218.382 – 214.746 = 3.636

Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa penambahan kasus terkonfirmasi terbesar berada pada rentang tanggal 9 September – 10 September, yakni sebanyak 3.861.

Jadi, jawaban yang tepat adalah B.

10. Topik: Menghitung Jumlah dalam Suatu Rentang Waktu

Perhatikan teks berikut!

Data Covid-19 Tahun 2022

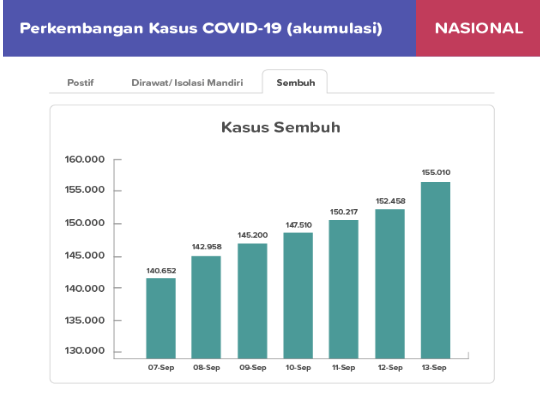
Per 1 September 2020, Indonesia telah melaporkan 177.571 kasus positif COVID-19, dengan catatan sebanyak 42.009 dirawat/isolasi mandiri, 128.057 sembuh, dan 7.505 meninggal. Case fatality ratio (CFR) adalah proporsi individu terkonfirmasi penyakit yang meninggal karena penyakit tersebut. Berikut merupakan data perkembangan kasus pasien COVID-19.

Jangkauan data berdasarkan grafik kasus sembuh pada rentang tanggal 7 September 2020 – 13 September 2020 adalah ….

1. 14.358
2. 25.552
3. 140.652
4. 152.458
5. 155.010

Jawaban: A

Pembahasan: 

Data terendah = 140.652

Data tertinggi = 155.010

Jangkauan data adalah selisih data dengan nilai terbesar dan nilai terkecil.

Jangkauan data = data tertinggi – data terendah

Jangkauan data = 155.010 – 140.652

Jangkauan data = 14.358

Jadi, jawaban yang tepat adalah A.

11. Perhatikan gambar berikut ini!

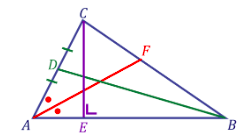
Terdapat garis istimewa pada sebuah segitiga, yaitu garis tinggi, garis bagi, dan garis berat dengan definisi masing-masing garis sebagai berikut.

• Garis tinggi adalah garis lurus yang menghubungkan salah satu titik sudut segitiga ke sisi di hadapannya secara tegak lurus.

• Garis bagi adalah garis yang dibuat dari salah satu titik sudut segitiga dan membagi sudut tersebut menjadi dua bagian sama besar.

• Garis berat adalah garis yang menghubungkan salah satu titik sudut segitiga ke sisi di hadapannya dan membagi sisi tersebut menjadi dua bagian sama panjang.

Jika salah satu sisi adalah garis tinggi dan salah satu garis bagi juga berperan sebagai garis berat, jenis segitiga yang dimaksud adalah ….

1. segitiga siku-siku sama kaki 
2. segitiga sembarang
3. segitiga sama kaki
4. segitiga sama sisi
5. segitiga siku-siku

Jawaban: A

Pembahasan:

Segitiga yang dimaksud memiliki kriteria sebagai berikut.

• Salah satu sisi adalah garis tinggi.

• Salah satu garis bagi adalah garis berat.

Garis tinggi adalah garis tegak lurus yang menghubungkan salah satu titik sudut segitiga ke salah satu sisi segitiga.

Diketahui salah satu sisi merupakan garis tinggi. Akibatnya, terdapat dua sisi segitiga yang saling tegak lurus. Segitiga dengan kriteria ini adalah segitiga siku-siku.

Kemudian, diketahui salah satu garis bagi juga berperan sebagai garis berat. Garis bagi membagi sudut sama besar, sedangkan garis berat membagi sisi sama panjang.

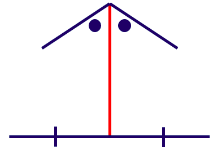
Kesimpulan sebelumnya menyatakan bahwa segitiga yang dimaksud merupakan segitiga siku-siku. Sudut siku-siku yang mungkin adalah sudut yang dibagi oleh garis bagi yang ditandai warna merah.

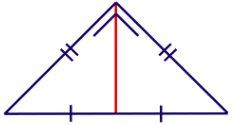
Dengan demikian, segitiga yang dimaksud adalah segitiga siku-siku sama kaki.

Jadi, jawaban yang benar adalah A.

12. Berdasarkan perspektif ekonomi, usia penduduk dikategorikan menjadi dua bagian, yaitu usia produktif (15—59 tahun) dan usia tidak produktif (di bawah 15 tahun dan 60 tahun ke atas). Jumlah penduduk pada suatu negara tahun 2021 tercatat sebagai berikut.

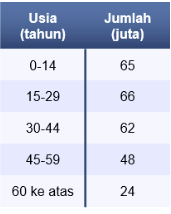
Persentase penduduk yang berada pada kategori usia tidak produktif di negara tersebut adalah sekitar ….

1. 9,05%
2. 24,52%
3. 33,58%
4. 42,25%
5. 66,67%

Jawaban: C

Pembahasan:

Berdasarkan informasi pada soal, kategori penduduk tidak produktif meliputi kelompok usia di bawah 15 tahun dan 60 tahun ke atas. Oleh karena itu, jumlah penduduk dari kedua kelompok usia tersebut adalah sebagai berikut.

n (tidak produktif) = 65 + 24

                               = 89

Sementara itu, jumlah seluruh penduduk di negara tersebut adalah sebagai berikut.

n (total) = 65 + 66 + 62 + 48 +24

              = 265

Persentase penduduk dengan kategori usia tidak produktif dapat dihitung sebagai berikut.

Dengan demikian, persentase penduduk yang berada pada usia tidak produktif adalah sekitar 33,58%.

Jadi, jawaban yang benar adalah C.

14. Perhatikan ilustrasi berikut!

Gedung Teater

Dalam suatu gedung teater di Provinsi Suka-Suka terdapat 11 baris kursi. Baris pertama berisi 10 kursi, baris kedua berisi 15 kursi, baris ketiga berisi 17 kursi, baris keempat berisi 22 kursi, baris ke lima berisi 24 kursi, dan seterusnya mengikuti pola yang sama. Berdasarkan informasi tersebut, banyaknya kursi pada baris kedua dari belakang adalah … kursi.

1. 31
2. 36
3. 38
4. 43
5. 45

Jawaban: D

Pembahasan:

Pola susunan kursi pada gedung teater tersebut dapat diuraikan sebagai berikut.

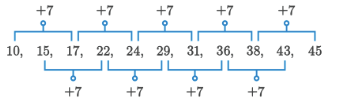
Berdasarkan pola tersebut, dapat disimpulkan bahwa banyaknya kursi yang berada pada baris kedua dari belakang atau baris kesepuluh adalah 43 kursi.

Jadi, jawaban yang tepat adalah D.

14. Topik: Aljabar

Subtopik: Konsep Kilat Aritmatika Sosial 

Perhatikan informasi berikut!

Pajak Penghasilan (PPh) berdasarkan UU PPh didefinisikan sebagai pajak yang dikenakan kepada orang pribadi atau badan atas penghasilan yang diperoleh dalam tahun pajak. Untuk Penghasilan Tidak Kena Pajak (PTKP), karyawan yang memiliki status belum menikah dan tidak memiliki tanggungan adalah Rp54.000.000,00 per tahun. PPh termasuk ke dalam pajak progresif sehingga tarif pajak yang akan makin naik sesuai dengan naiknya dasar pengenaan pajak. Diketahui perhitungan tarif PPh berdasarkan pasal 21 sesuai UU PPh didasari oleh Penghasilan Kena Pajak (PKP) dan disajikan dalam tabel berikut.

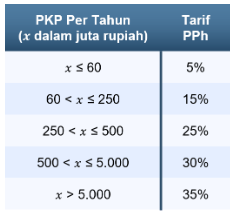
Sebagai contoh, untuk penghasilan Andi setelah dikurangi PTKP adalah Rp300.000.000,00 per tahun, maka dikenakan tarif pajak sampai lapis ketiga, yaitu 25%. Pada tarif lapis pertama, Rp60.000.000,00 pertama dikenakan tarif pajak 5%. Kemudian, pada tarif lapis kedua, Rp190.000.000,00 berikutnya (dari 60 juta sampai 250 juta) dikenakan tarif pajak 15%. Selanjutnya, pada tarif lapis terakhir, sisa Rp50.000,000 dikenakan tarif pajak 25%.

John adalah seorang guru dengan status belum menikah dan tidak memiliki tanggungan dengan penghasilan netto sebesar Rp4.000.000,00 per bulan. Tarif pajak tahunan yang harus dibayar oleh John adalah ….

1. Rp0,00
2. Rp200.000,00
3. Rp300.000,00
4. Rp2.400.000,00
5. Rp2.700.000,00

Jawaban: A

Pembahasan:

Misalkan penghasilan John selama 1 tahun adalah P, maka besarnya dalam setahun adalah sebagai berikut.

Karena Penghasilan Tidak Kena Pajak (PTKP) karyawan yang memiliki status belum menikah dan tidak memiliki tanggungan adalah Rp54.000.000,00 per tahun dan penghasilan John selama 1 tahun hanya Rp48.000.000,00, maka John tidak berkewajiban membayar pajak.

Dengan demikian, tarif pajak tahunan yang harus dibayar oleh John adalah Rp0,00.

15. Topik: Data dan Ketidakpastian

Subtopik: Konsep Kilat Statistika Deskriptif

Perhatikan informasi berikut!

Berdasarkan perspektif ekonomi, usia penduduk dikategorikan menjadi dua bagian, yaitu usia produktif (15—59 tahun) dan usia tidak produktif (di bawah 15 tahun dan 60 tahun ke atas). Jumlah penduduk pada suatu negara tahun 2021 tercatat sebagai berikut.

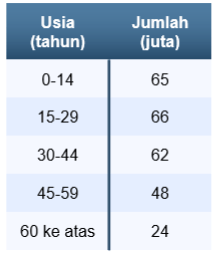
Persentase penduduk yang berusia 30—44 tahun terhadap jumlah seluruh penduduk yang berada pada usia produktif adalah sekitar ….

1. 37,50%
2. 35,23%
3. 31,52%
4. 27,28%
5. 24,22%

Jawaban: B

Pembahasan:

Kategori penduduk usia 30—44 tahun atau dapat ditulis n(30-44) merupakan kategori usia produktif dengan jumlah penduduk sebesar 62 juta jiwa.

Sementara itu, penduduk yang berada pada usia produktif merupakan penduduk dengan kelompok usia 15—59 tahun dengan jumlah penduduk sebagai berikut.

Persentase penduduk yang berusia 30—44 tahun terhadap jumlah seluruh penduduk yang berada pada usia produktif dapat dihitung sebagai berikut.

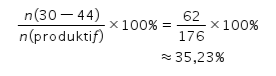
Dengan demikian, persentase penduduk yang dimaksud adalah sekitar 35,23%.

Itulah 15 contoh soal UTBK SNBT 2025 penalaran matematika beserta pembahasannya yang bisa dijadikan sebagai bahan belajar.