Memahami Materi Persamaan Kuadrat, Rumus dan Contoh Soalnya

Materi persamaan kuadrat merupakan persamaan polynomial atau suku banyak yang pangkat tertingginya 2 atau berode 2. Persamaannya bisa dilihat dalam olahraga seperti bermain basket, memanah, sepak bola, dan lainnya.
Ketika pemain melepaskan tembakan, lintasan tembakkan tidak membentuk garis lurus melainkan melengkung atau kurva. Gerakan yang dihasilkan tersebut disebut parabola yang merupakan salah satu bentuk grafik persamaan kuadrat,
Pengertian dan Bentuk Umum Materi Persamaan Kuadrat
Terdapat banyak persamaan dalam mata pelajaran Matematika, salah satunya persamaan kuadrat. Persamaan kuadrat yaitu persamaan suku banyak dengan dua pangkat lebih tinggi.
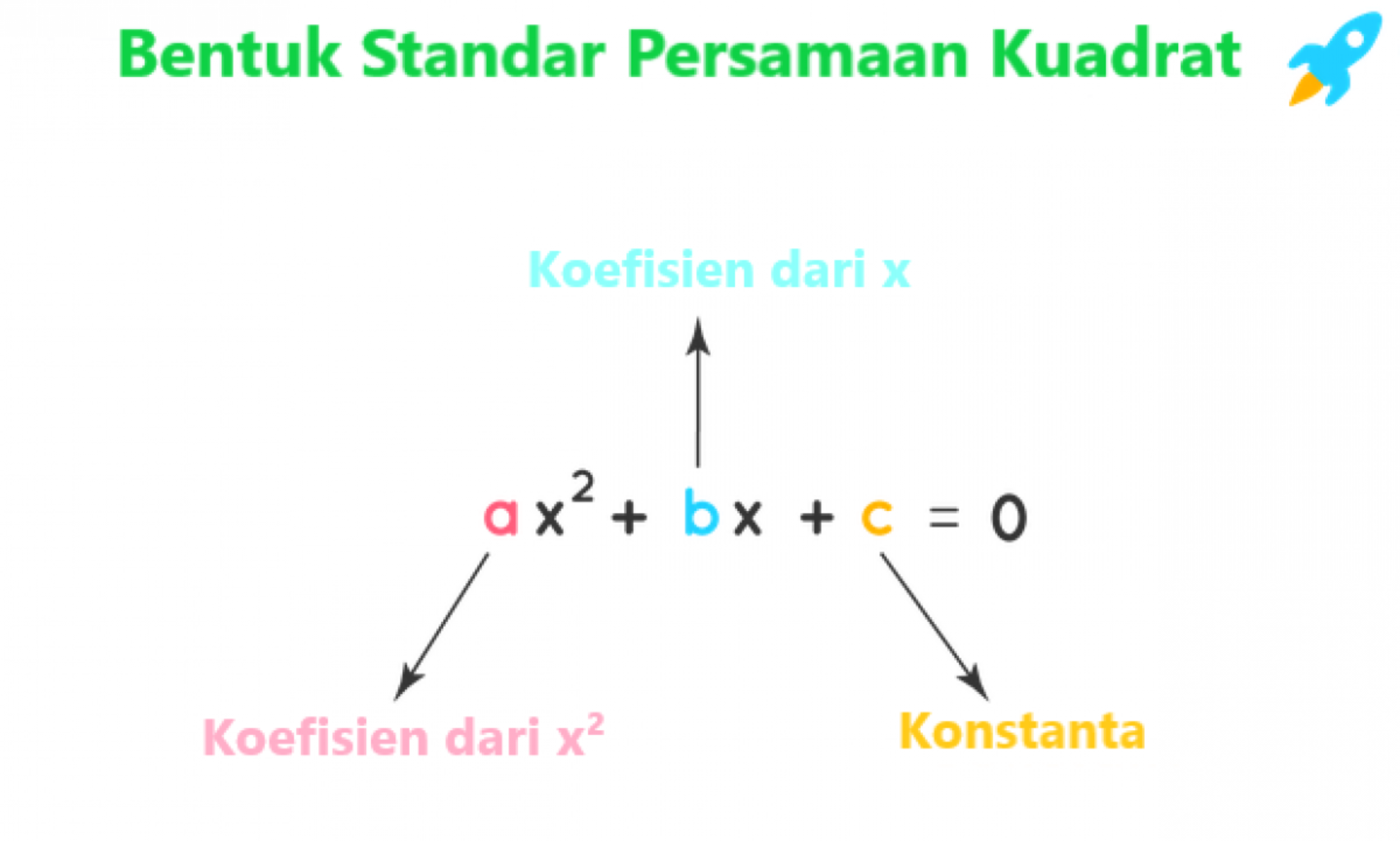
Jenis persamaan kuadrat dikenal dengan persamaan berorder 2. Tentunya berbeda dengan persamaan linier, pangkat tertinggi persamaan linier yaitu 1. Berikut bentuk umum rumus persamaan kuadrat:
Ax2 + bx + c = 0
Dalam persamaan tersebut, a, b dan c termasuk bilangan real. Sedangkan a tidak sama dengan 0. Kemudian x merujuk variabel yang nilainya belum diketahui.
Cara Menyelesaikan Persamaan Kuadrat
Untuk menentukan nilai x yang memenuhi persamaan kuadrat diperoleh dari hasil substitusi sama dengan 0 (nol), biasa disebut akar persamaan kuadrat. Umumnya ada 2 akar persamaan kuadrat yang diperoleh. Untuk menentukan akar persamaan kuadrat, berikut 3 caranya:
1. Cara Memfaktorkan Persamaan Kuadrat
ax2+bx+c=0 menjadi (rx-p) (sx+q)=0
Adapun contoh soal faktorisasi kuadrat yaitu sebagai berikut,
Akar-akar persamaan kuadrat 6x^2+13x-5= 0 adalah…
Pembahasan:
Persamaan kuadrat dapat diselesaikan dengan cara memfaktorkan
6x^2+ 13x-5= 0
(3x −1)(2x +5)= 0
3x=1 atau 2x =−5
x1= 1/3 atau x2= -5/2
Akar persamaan kuadrat di atas diperoleh {- 5/2 , 1/3 }
2. Kuadrat Sempurna
Melengkapi kuadrat sempurna merupakan metode dengan mengubah bentuk umum jadi kuadrat sempurna seperti ini:
〖(x+1)〗^2 atau 〖(2x-3)〗^2
Metode tersebut mengubah bentuk 〖ax〗^2+ bx+ c= 0 menjadi bentuk berikut:
x^2+bx+(b/2 )^2= (b/2 )^2 - C
(x+ b/2 )^2= (b/2 )^2 – C
Contoh soal materi persamaan kuadrat sempurna:
Tentukan penyelesaian dari x⌃(2) – 2x + 1= 7, lengkapi kuadrat sempurna tersebut!
Pembahasan: x⌃(2) – 2x + 1= 7
(x-1) ⌃(2)= 7
(x-1) ⌃(2)= sqrt(7)
x= pm sqrt (7) + 1
x_(1) = sqrt(7) + 1 atau x_(2)= -
sqrt(7) + 1
3. Rumus ABC Persamaan Kuadrat
Rumus ABC meerupakan salah satu rumus yang digunakan untuk mencari akar-akar dalam persamaan kuadrat. Rumus ABC digunakan untuk melengkapi kuadrat sempurna yang tidak bisa dilakukan, biasanya digunakan saat pemfaktoran.
Bagi sebagian orang, rumus ABC dijadikan sebagai metode untuk mendapatkan nilai akar persamaan kuadrat. Berikut rumusnya:
x=(-b±√(b^2-4ac))/2a
a ≠ 0
Dalam rumus persamaan kuadrat, a, b, dan c= Bilangan real dan konstanta
x = variabel
Untuk bisa digunakan dalam menyelesaikan permasalahan kuadrat, rumus ABC memiliki beragam peraturan. Peraturan ini memiliki fungsi agar rumus ABC bisa disesuaikan dan tepat sasaran, berikut di antaranya:
- Dalam rumus ABC diperoleh nilai diskriminan yaitu d sudah diterapkan dalam rumus ABC: b2 – 4ac
- Nilai a jangan sama dengan 0 atau a≠0
- Jika nilai D < 0 maka nilai akarnya tidak real
- Jika nilai D > 0 maka nilai akarnya dikatakan real dengan catatan x1, x2 R, nilai x1 tidak boleh sama dengan nilai x2 atau x1 ≠ x
- Jika nilai D=0 maka akar-akarnya dikatakan real dengan catatan x1, x2 R, nilai x1 sama dengan nilai x2 atau x1 = x
Contoh soal rumus ABC persamaan kuadrat:
Coba tentukan akar dari persamaan x2 + 8x + 12 = 0 menggunakan rumus ABC!
Pembahasan:
x1,2=(-b±√(b^2-4ac))/2a
x1,2= (-8±√(8^2-4(1)(12)))/(2(1))
x1,2= (-8±√(64-48))/2
x1,2= (-8±√16)/2
x1,2= (-8±4)/2
x1,2= (-4±2)¦
x1= -4-2= -6
x2= -4+2= -2
Bisa disimpulkan akar dari x1 = -6 atau x2 = -2, bentuk himpunannya yaitu sebagai berikut:
HP = {-6,-2}
Untuk memahami materi persamaan kuadrat perlu melatih mencoba menyelesaikan beberapa contoh soalnya. Sebab memahami rumus Matematika tidak sama dengan teori dalam mata pelajaran lain sehingga perlu banyak latihan.