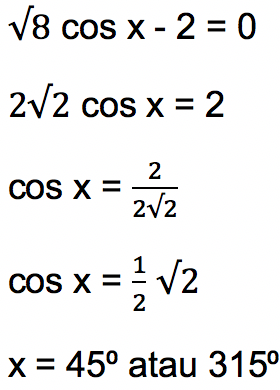Memahami Perbandingan Trigonometri Sudut Istimewa
Dalam mata pelajaran SMA, siswa akan mempelajari materi trigonometri. Ini suatu cabang ilmu matematika yang mempelajari mengenai sudut, sisi, dan perbandingan antara sudut terhadap sisi.
Untuk memudahkan menentukan perbandingan trigonometri pada segitiga siku-siku, dapat digunakan sindemi, cosami, tandesa, dan sebagainya.
Dalam trigonometri, ada istilah yang disebut dengan sudut istimewa, yang artinya adalah sudut-sudut yang nilai perbandingan trigonometrinya dapat ditentukan secara eksak, tanpa memakai kalkulator atau tabel matematika.
Untuk lebih jelasnya, simak pembahasan lengkapnya berikut ini.
Pengertian Sudut Istimewa
Seperti penjelasan di atas, dalam materi rasio trigonometri, dikenal suatu istilah yang disebut sebagai sudut istimewa. Ini merupakan sudut-sudut khusus yang diperoleh dari keempat kuadran lingkaran dengan rentang 0⁰ sampai 360⁰.
Sudut ini dinamai demikian karena besar nilai perbandingan trigonometrinya bisa dihitung dengan mudah tanpa mengandalkan perhitungan dan kalkulator. Rasio atau perbandingan panjang sisi-sisi di sudut tertentu langsung diketahui dengan sudut istimewa trigonometri.
Sudut istimewa yang umum dikenal dalam trigonometri adalah 0⁰, 30⁰, 45⁰, 60⁰, 90⁰ yang terletak di kuadran I.
Namun, untuk memudahkan dalam mempelajari besar sudut istimewa dalam trigonometri, tabel di bawah ini menyajikan tabel perbandingan trigonometri pada sudut istimewa dari 0⁰ sampai 360⁰ (kuadran I sampai IV).
| Sudut | Sin | Cos | Tan |
| 0⁰ | 0 | 1 | 0 |
| 30⁰ | ½ | ½ √3 | ⅓ √3 |
| 45⁰ | ½ √2 | ½ √2 | 1 |
| 60⁰ | ½ √3 | ½ | √3 |
| 90⁰ | 1 | 0 | Tidak terdefinisi |
| 120⁰ | ½ √3 | -½ | -√3 |
| 135⁰ | ½ √2 | -½ √2 | -1 |
| 150⁰ | ½ | -½ √3 | -⅓ √3 |
| 180⁰ | 0 | -1 | 0 |
| 210⁰ | -½ | -½ √3 | ⅓ √3 |
| 225⁰ | -½ √2 | -½ √2 | 1 |
| 240⁰ | -½ √3 | -½ | √3 |
| 270⁰ | -1 | 0 | Tidak terdefinisi |
| 300⁰ | -½ √3 | ½ | -√3 |
| 315⁰ | -½ √2 | ½ √2 | -1 |
| 330⁰ | -½ | ½ √3 | -⅓ √3 |
| 360⁰ | 0 | 1 | 0 |
Dalam Kuadran I, II, III, IV
Lingkaran memiliki total sudut sebesar 360⁰. Sudut pada lingkaran tersebut kemudian dibagi ke dalam empat buah kuadran dimanasSetiap kuadran tersebut mempunyai rentang besar sudut sebesar 90⁰.
1. Kuadran I
Kuadran I terletak di sisi kanan atas lingkaran yang memiliki rentang ukuran sudut mulai dari 0⁰ sampai 90⁰. Pada kuadran I ini terdapat sudut-sudut istimewa yakni 0⁰, 30⁰, 45⁰, 60⁰, 90⁰. Nilai sinus (sin), cosinus (cos) dan tangen pada kuadran I bertanda positif
2. Kuadran II
Kuadran II terletak di sebelah kiri atas lingkaran dengan rentang ukuran sudut mulai dari 90⁰ sampai 180⁰. Pada kuadran II terdapat sudut istimewa 120⁰, 135⁰, 150⁰, 180⁰. Pada kuadran II, nilai sinus positif sementara cosinus dan tangen bernilai negatif.
3. Kuadran III
Kuadran III terletak di sebelah kiri bawah lingkaran dengan rentang ukuran sudut mulai dari 180⁰ sampai 270⁰. Pada kuadran III terdapat sudut-sudut istimewa yaitu 210⁰, 225⁰, 240⁰, 270⁰. Pada kuadran III mempunyai nilai cosinus dan sinus negatif sementara tangen bernilai positif.
4. Kuadran IV
Kuadran IVI terletak di sebelah kanan bawah lingkaran dengan rentang ukuran sudut mulai dari 270⁰ sampai 360⁰. Pada kuadran IV terdapat sudut-sudut istimewa yaitu 300⁰, 315⁰, 330⁰, 360⁰. Pada kuadran IV mempunyai nilai tangen dan sinus negatif sementara cosinus bernilai positif.
Tabel Trigonometri
Di bawah ini merupakan tabel trigonometri yang berisi rumus trigonometri sin, cos, tangen, secan, cosecant dan cotangent untuk berbagai sudut di keempat kuadran.
kuadran.
| Kuadran I | Kuadran II | Kuadran III | Kuadran IV | |
| Cos a | Sin (90⁰ – a) | -Cos (180⁰ – a) | -Cos (180 + a) | Cos (360⁰ – a) |
| Sin a | Cos (90⁰ – a) | Sin (180⁰ – a) | -Sin (180 + a) | -Sin (360⁰ – a) |
| Tan a | Cotan (90⁰ – a) | -Tan (180⁰ – a) | Tan (180⁰ + a) | -Tan (360⁰ – a) |
| Sec a | Cosec (90⁰ – a) | -Sec (180⁰ – a) | -Sec (180⁰ + a) | Sec (360⁰ – a) |
| Cosec a | Sec (90 – a) | Cosec (180 – a) | -Cosec (180⁰ + a) | -Cosec (360⁰ – a) |
| Cotan a | Cotan (90⁰ – a) | -Cotan (180⁰ – a) | Cotan (180⁰ + a) | -Cotan (360⁰ – a) |
Perbandingan Trigonometri Sudut Istimewa
Perbandingan trigonometri sudut istimewa adalah perbandingan trigonometri sinus (sin), cos, tangen, secan, cosecan dan tangen pada sudut 0⁰, 30⁰, 45⁰, 60⁰, dan 90⁰. Berikut adalah tabel perbandingan trigonometri dari sudut khusus.
| Sudut | Sin | Cos | Tan | Secan | Cosecan | Cotangen |
| 0⁰ | 0 | 1 | 0 | 1 | Tidak terdefinisi | Tidak terdefinisi |
| 30⁰ | ½ | ½ √3 | ⅓ √3 | √3 | 2 | √3 |
| 45⁰ | ½ √2 | ½ √2 | 1 | √2 | √2 | 1 |
| 60⁰ | ½ √3 | ½ | √3 | 2 | √3 | ⅓ √3 |
| 90⁰ | 1 | 0 | Tidak terdefinisi | Tidak terdefinisi | 1 | 0 |
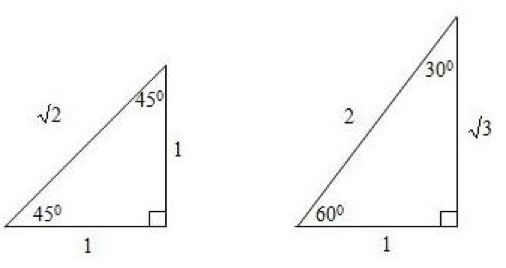
Apabila digambarkan ke dalam bangun segitiga siku-siku, maka sudut khusus akan membentuk perbandingan sisi segitiga seperti gambar di bawah ini.
Contoh Soal Perbandingan Trigonometri Sudut Istimewa
Berikut di bawah ini beberapa contoh soal tentang perbandingan trigonometri sudut istimewa yang bisa dipelajari.
Contoh Soal 1
Tentukanlah nilai dari sin 120°+cos 201°+cos 315°!
Jawab:
sin 120° ada di kuadran II, hingga nilainya tetap positif dengan besar sama seperti sin 60°
sin 120° = sin (180-60)° = sin 60° = 1/2 √3
cos 120° ada di kuadran III, hingga nilainya negatif dengan besar sama seperti cos 30°
cos 120° = cos (180+30)° = – cos 30° = -1/2 √3
cos 315° ada di kuadran IV, hingga nilainya positif dengan besar sama seperti cos 45°
cos 315° = cos (360-45)° = cos 45° = 1/2 √2
Contoh Soal 2
Diketahui segitiga siku-siku ABC, siku-siku di C, panjang a = 4 dan b = 3.Tentukanlah panjang sisi dan nilai perbandingan trigonometri sudut α
Jawab:

Contoh Soal 3
Tentukan berapa besar sudut x yang memenuhi persamaan trigonometri dari √12 tan x – 2 = 0
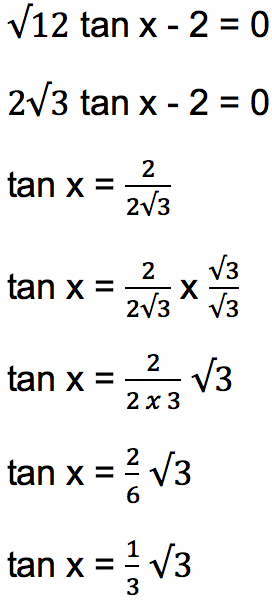
Besar nilai x yang memenuhi persamaan
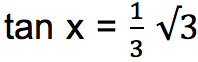
dengan mengecek tabel sin cos tan yakni x = 30⁰ dan x = 210⁰
Contoh Soal 4
Tentukan berapakah nilai dari perbandingan trigonometri sudut A segitiga siku-siku ABC, yang mana sisi a memiliki panjang = 8 cm dan sisi b = 6 cm. Sudut siku-siku berada di titik C.
Jawab:
Pertama-tama harus dihitung terlebih dahulu panjang sisi c menggunakan persamaan phytagoras sudut siku-siku:
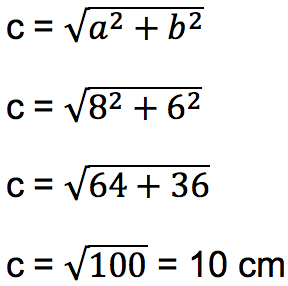

Contoh Soal 5
Tentukan besar sudut x dari persamaan trigonometri √8 cos x – 2 = 0
Jawab: