Metode Penyelesaian dan Contoh Soal SPLDV yang Bisa Dipelajari Siswa

Dalam mata pelajaran matematika SMA, siswa akan mempelajari sistem persamaan linear dua variabel atau SPLDV. Dikutip dari laman Zenius, SPLDV adalah suatu persamaan matematika yang terdiri atas dua persamaan linear (PLDV), yang masing-masing bervariabel dua, misalnya variabel x dan variabel y.
SPLDV memiliki empat ciri, yakni terdiri dari 2 variabel, hanya memiliki derajat satu atau berpangkat satu, menggunakan relasi tanda sama dengan (=), dan tidak terdapat perkalian variabel dalam setiap persamaannya.
Secara umum, SPLDV dituliskan dengan bentuk ax + by = c, dimana 'x' dan 'y' adalah variabel dengan peringkat satu, 'a' dan 'b' adalah koefisien, serta 'c' adalah konstanta.
Dalam kehidupan sehari-hari, sistem persamaan linear dua variabel memiliki banyak fungsi antara lain menghitung keuntungan atau laba, mencari harga dasar atau harga pokok suatu barang, dan membandingkan harga barang. Untuk memahami lebih mendalam tentang materi matematika, simak ulasan lengkapnya dibawah ini.
Metode Penyelesaian SPLDV
1. Metode Grafik
2. Metode Substitusi
Merupakan metode yang dilakukan dengan memasukkan salah satu variabel ke variabel lain
X + y = 3 => y = 3 – x .....(2)
Substitusikan persamaan dua ke persamaan pertama
X + 2 (3-x) = 4
X + 6 – 2 x = 4
-x = 4 – 6
-x = -2
X = 2
Substitusikan x = 2 ke persamaan 2 maka y = 3 – 2 = 1
3. Metode Eliminasi
4. Metode Gabungan Eliminasi dan Substitusi
Contoh Soal SPLDV
Berikut dibawah ini beberapa contoh soal SPLDV dari berbagai sumber yang bisa dipelajari agar paham penerapan rumusnya yang baik dan benar.
Contoh Soal 1
Tentukan nilai variabel x dan y dari persamaan berikut
x + 2y = 20
2x + 3y = 33
Dengan menggunakan metode eliminasi!
Jawaban:
Pertama, cari nilai variabel x dengan cara menghilangkan y pada masing-masing persamaan.
x + 2y = 20
2x + 3y = 33
Koefisien pada variabel y dari masing-masing persamaan tersebut adalah 2 dan 3.
Selanjutnya kita cari KPK (kelipatan persekutuan terkecil) dari 2 dan 3.
2 = 2, 4, 6, 8, …
3 = 3, 6, 8, …
Setelah tahu KPK dari 2 dan 3 adalah 6, kita bagi 6 dengan masing masing koefisien.
6 : 2 = 3 → x3
6 : 3 = 2 → x2
Kemudian, kalikan dan lakukan eliminasi dengan menggunakan hasil pembagian masing-masing tadi
x + 2y = 20 | x3
2x + 3y = 33 _ | x2
Maka menghasilkan:
3x + 6y = 60
4x + 6y = 66 _
-x = -6
x = 6
Contoh Soal 2
Tentukan penyelesaian dari persamaan 3x+ 5y = 16 , dan 4x + y = 10 , apabila x = a dan y = b . Maka tentukanlah nilai a dan b nya !
Penyelesaiannya :
Diketahui :
Persamaan 1 = 3x+ 5y = 16
Dan Persamaan 2 = 4x + y = 10
Langkah yang Pertama yaitu tentukanlah variabelnya yang mana akan di eliminasi terlebih dahulu perhatikan penyelesaian di bawah ini :
3x+ 5y = 16 | x1 | <=> 3x + 5y = 16 . . . . (1)
4x + y = 10 | x5 | <=> 20x + 5y = 50 . . . (2)
Dari persamaan (1) dan juga (2), dapat kita eliminasikan dan dapat menghasilkan yaitu :
20x + 5y = 50
3x + 5y = 16 _
17 x + 0 = 34
x = 34 / 17
x = 2
Langkah yang Kedua selanjutnya, marilah kita lakukan langkah yang sama namun kali ini harus sama dengan x nya , maka caranya yaitu sebagai berikut :
3x+ 5y = 16 | x4 | <= > 12 x + 20y = 64 . . .(3)
4x + y = 10 | x3 | <=> 12x + 3y = 30 . . . .(4)
Langkah yang Ketiga Persamaan (3) dan juga (4) , marilah kita eliminasikan untuk menghasilkan nilai y nya :
12 x + 20y = 64
12x + 3y = 30 _
0 + 17y = 34
y = 2
Jadi , Himpunannya = { 2 ,2 } , dan pada nilai a dan b yaitu : a= x = 2 dan b = y = 2
Contoh Soal 3
Contoh Soal 4
Tentukan himpunan penyelesaian dari persamaan x + 3y = 15 dan 3x + 6y = 30
Jawaban:
Sederhanakan terlebih dahulu satu persamaan, yaitu 3x + 6y = 30 dibagi 3 menjadi x + 2y = 10
Kemudian eliminasi persamaan:
x + 3y = 15
x + 2y = 10
Hasilnya adalah y = 5
Eliminasi kembali untuk mencari nilai x dengan mengalikan 2 pada persamaan x + 3y = 15 menjadi 2x + 6y = 30
Kemudian eliminasi persamaan:
3x + 6y = 30
2x + 6y = 30
Hasilnya adalah x = 0
Himpunan penyelesaian adalah {0, 5}
Contoh Soal 5
Carilah himpunan penyelesaian dari SPLDV berikut ini:
3x + 2y = 10
9x – 7y = 43
Jawaban:
Langkah 1, nyatakan ke dalam variabel y :
3x + 2y = 10
y = 1/2 (10 - 3x)
y = 5 - 3x/2
Langkah 2, subsitusikan nilai y dan temukan nilai x
9x – 7y = 43
9x - 7(5 - 3x/2) = 43
9x - 35 + 21x/2 = 43 (persamaan dikalikan 2 untuk menghilangkan pecahan)
18x - 70 + 21x = 86
39x - 70 = 86
39x = 156
x = 4
Langkah 3, subsitusikan nilai x ke dalam persamaan
x = 4 ↔ y = 5 - 3x/2
y = 5 - 3(4)/2
y = 5 - 12/2
y = 5 - 6
y = -1
Jadi, himpunan penyelesaiannya adalah { 4 , -1 }
Contoh Soal 6
Contoh Soal 7
Tentukan himpunan dari penyelesaian dan dari persamaan berikut ini yaitu x + 3y = 15 dan 3x + 6y = 30 ?
Penyelesaiannya :
Diketahui :
Persamaan Pertama = x + 3y = 15
Persamaan yang Kedua = 3x + 6y = 30
Langkah yang Pertama : Ubahlah dari salah satu persamaan dan carilah yang termudah.
X + 3y = 15 —> X = -3y + 15
Langkah yang Kedua : Subsititusi nilai X = -3y + 15 ke dalam persamaan yang kedua untuk mencari nilai Y, maka hasilnya sebagai berikut yaitu :
3x + 6y = 30
3 (-3y +15) + 6y = 30
-9y + 45 + 6y = 30
-3y = 30 – 45
-3y = -15
y = 5
Langkah yang Ketiga : Selanjutnya carilah nilai x maka, gunakanlah salah satu dari persamaan boleh itu dari persamaan yang pertama maupun yang kedua :
Dari Persamaan yang Pertama :
+ 3y = 15
X + 3 (5) = 15
X + 15 = 15
X = 0
Persamaan yang Kedua :
3x + 6y = 30
3x + 6 (5) = 30
3x + 30 = 30
3x = 0
X = 0
Langkah yang Keempat : Maka nilai himpunannya jadi, = { 0 , 5 }
Contoh Soal 8
Tentukan penyelesaian dari persamaan 3x+ 5y = 16, dan 4x + y = 10, apabila x = a dan y = b. Maka tentukanlah nilai a dan b nya!
Contoh Soal 9
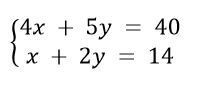
Penyelesaian
- Tentukan titik perpotongan tiap-tiap persamaan terhadap sumbu X dan Y.
Untuk 4x + 5y = 40
Titik perpotongan terhadap sumbu X (y=0)
= 4x + 5(0) = 40
= 4x + 0 = 40
=x = 40/4 = 10
Jadi, garis berpotongan dengan sumbu X di (10,0)
Titik perpotongan terhadap sumbu Y (x=0)
= 4(0) + 5y = 40
= 0 + 5y = 40
=y= 40/5= 8
Jadi, garis berpotongan dengan sumbu Y di (0,8)
Untuk x + 2y = 14
Titik perpotongan terhadap sumbu X (y=0)
= x + 2(0) = 14
= x + 0 = 14
= x = 14
Jadi, garis berpotongan dengan sumbu X di (14,0)
Titik perpotongan dengan sumbu Y (x=0)
= 0 + 2y =14
= 2y = 14
= y = 14/2 = 7 Jadi, garis berpotongan terhadap sumbu Y di (0,7)
- Gambarkan tiap-tiap persamaan dalam sebuah koordinat Kartesius.
- Jika sudah digambar, Anda akan mendapat perpotongan di titik (x,y) = (2,6)








