Rumus Volume Prisma Belah Ketupat dan Cara Menghitung Luas Permukaan

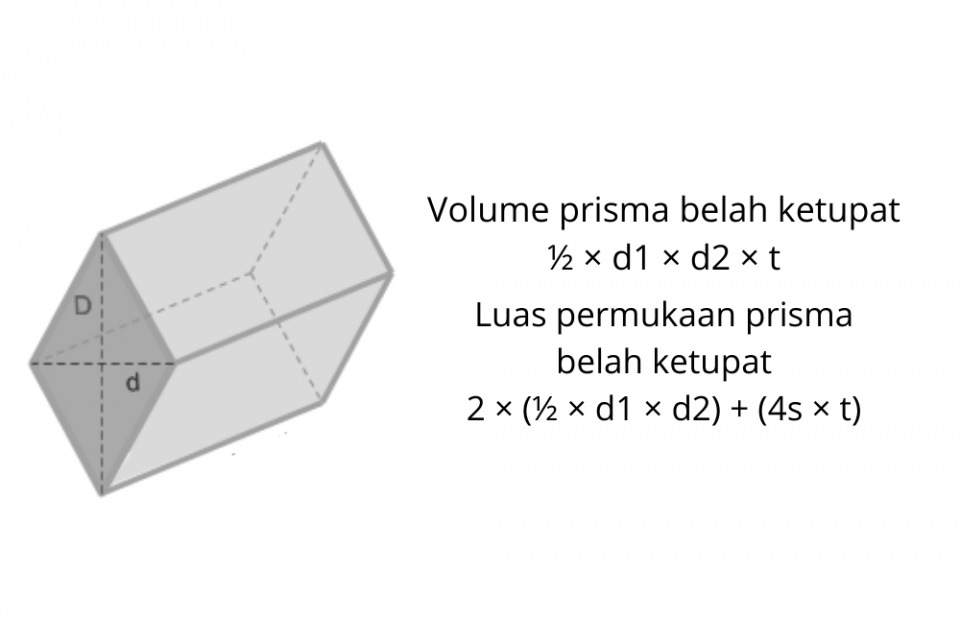
Prisma adalah bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup yang berbentuk sama dengan sisi-sisi tegak berbentuk persegi atau persegi panjang. Prisma mempunyai penampang melintang yang selalu sama dalam bentuk dan ukuran.

Dalam bangun ruang prisma, bidang alas dan atas sejajar serta kongruen. Bentuk prisma belah ketupat adalah bangun ruang yang memiliki alas dan atap berbentuk belah ketupat. Selimut prisma belah ketupat berbentuk persegi panjang.

Prisma belah ketupat memiliki 6 sisi, 12 rusuk, 12 diagonal sisi, 4 diagonal ruang, dan 6 bidang diagonal. Pembahasan materi matematika mengenai rumus volume dan luas permukaan prisma belah ketupat dapat disimak sebagai berikut.

Rumus Volume Prisma Belah Ketupat

Volume prisma dapat dihitung dengan mengetahui luas alas dan tinggi. Rumus volume prisma belah ketupat adalah ½ × d1 × d2 × t. Maka, diperlukan panjang kedua diagonal serta tinggi untuk mengetahui  volume prisma belah ketupat. Satuan volume ditulis dengan simbol pangkat tiga, misalnya cm³ atau m³.

Contoh soal:

Sebuah prisma belah ketupat ABCD dengan panjang diagonal AC = 10 cm, BD = 12 cm, dan tingginya 3 cm. Hitung volume prisma tersebut!

Pembahasan:

Diketahui: AC = 10; BD = 12; t = 3 cm

V = ½ × d1 × d2 × t

V = ½ × 10 × 12 × 3

V = 180 cm³

Jadi, volume prisma belah ketupat tersebut adalah 180 cm³.

Rumus Luas Permukaan Prisma Belah Ketupat

Luas permukaan prisma adalah jumlah kedua alas dan selimut (sisi tegak). Rumus luas permukaan prisma belah ketupat adalah 2 × luas alas + (keliling alas × tinggi) atau L = 2 × (½ × d1 × d2) + (4s × t). Keterangan:

L = Luas permukaan prisma

d1 dan d2 = Panjang diagonal alas

s = Panjang sisi

t = Tinggi prisma

Contoh soal:

1. Sebuah prisma belah ketupat memiliki diagonal alas 12 cm dan 16 cm. Panjang sisinya adalah 10 cm dan tingginya 5 cm. Hitung luas permukaan prisma tersebut.

Pembahasan:

Diketahui: d1 = 12 cm; d2 = 16 cm; s = 10 cm; t = 5 cm

Gunakan rumus luas permukaan prisma belah ketupat.

L = 2 × (½ × d1 × d2) + (4s × t)

L = 2 × (½ × 12 × 16) + (4(10) × 5)

L = 2 × (96) + (200)

L = 392 cm²

Jadi, luas permukaan prisma belah ketupat tersebut adalah 392 cm².

2. Sebuah prisma alasnya berbentuk belah ketupat dengan panjang diagonal 10 cm dan 24 cm. Tentukan tinggi prisma jika luas permukaannya 1.280 cm².

Diketahui: Lpermukaan = 1.280 cm2; d1 = 10 cm; d2 = 24 cm.

Ditanya: Tinggi prisma.

Gambar Alas Prisma Belah Ketupat (Katadata)

AO = OC = ½ × AC = 24÷2 cm = 12 cm

BO = OD = ½ × BD = 10÷2 cm = 5 cm

Sisi belah ketupat adalah sama panjang, sehingga dapat ditentukan panjang AD dengan menggunakan rumus phytagoras sebagai berikut:

AD² = AO² + OD²

AD² = 12² + 5²

AD² = 144 + 25

AD² = 169

AD = √169

AD = ± 13 cm

Setelah itu, hitung luas selimut prisma yang terdiri dari empat persegi panjang.

L = 4(13 × t) = 52 × t

Kemudian hitung luas belah ketupat.

L = 12 × 10 × 24 =120 cm²

Prisma belah ketupat terdiri dari dua bidang belah ketupat dan selimut. Maka, hitung luas permukaan prisma belah ketupat sebagai berikut.

Luas permukaan prisma = Luas dua bidang belah ketupat + luas selimut

1.280 = (120 × 2) + (52 × t)

1.280 = 240 + (52 × t)

1.280 - 240 = 52 × t

1040 ÷ 52 = t

t = 20 cm

Jadi, tinggi prisma belah ketupat adalah 20 cm.

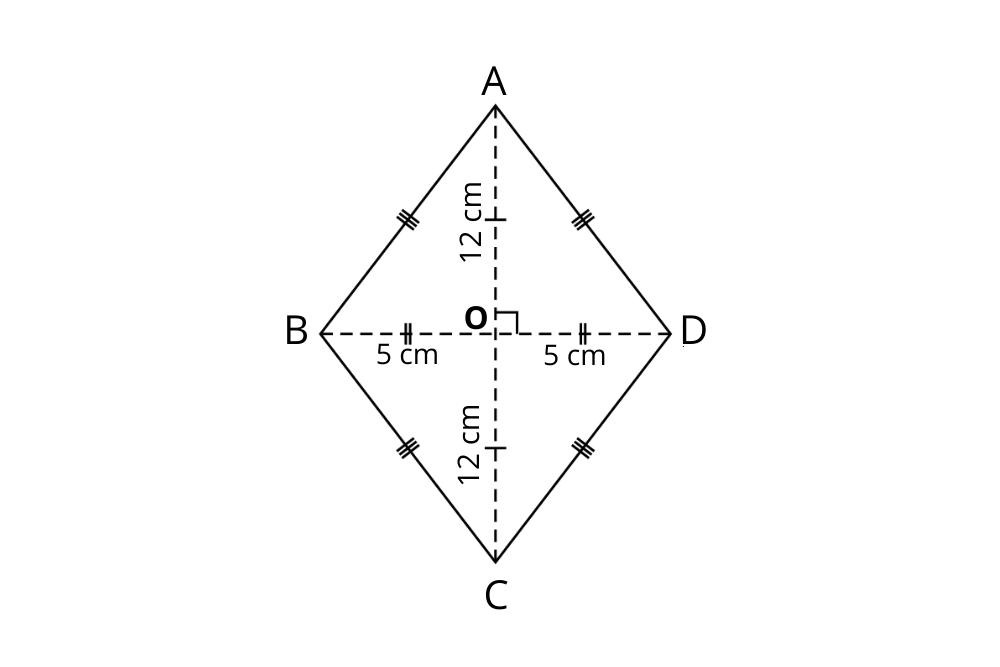
3. Keliling alas sebuah prisma yang berbentuk belah ketupat adalah 40 cm. Panjang salah satu diagonal alasnya adalah 12 cm. Tentukan volume prisma tersebut jika diketahui tinggi prisma adalah 15 cm!

Pembahasan:

Diketahui: K = 40 cm; d1 = 12 cm; t =15 cm.

Ditanya: Volume prisma

Cari panjang sisi prisma menggunakan rumus keliling belah ketupat.

K = 4s

40 = 4s

s = 10 cm

Perhatikan gambar berikut.

Gambar Alas Prisma Belah Ketupat (Katadata)

Diketahui panjang diagonal BD atau d1 adalah 12, maka panjang BO = DO = 6 cm. Untuk menghitung panjang diagonal lainnya, gunakan rumus phytagoras.

AO² = AD² - DO²

AO² = 10² - 6²

AO² = 100 - 36

AO² = 64

AO = √64

AO = 8 cm

Diketahui panjang AO = 8 cm, maka diagonal AC atau d2 adalah 16 cm. Setelah mengetahui panjang kedua diagonal dan tinggi prisma, maka gunakan rumus volume prisma belah ketupat.

V = ½ × d1 × d2 × t

V = ½ × 12 × 16 × 15

V = 1.440 cm³

Jadi, volume prisma belah ketupat tersebut adalah 1.440 cm³.

Unsur-Unsur Prisma Belah Ketupat

Unsur-unsur prisma belah ketupat meliputi:

• Sisi: Bidang yang membentuk dan membatasi bangun ruang. Terdapat 6 sisi dalam prisma belah ketupat.
• Rusuk: Ruas garis yang merupakan perpotongan dari dua bidang sisi bangun ruang. Ada 12 rusuk dalam prisma belah ketupat.
• Titik sudut: Pertemuan tiga buah rusuk. Prisma belah ketupat memiliki 8 titik sudut.
• Diagonal sisi: Ruas garis yang menghubungkan dua buah titik sidut yang saling berhadapan pada suatu sisi prisma. Terdapat 12 diagonal sisi dalam prisma belah ketupat.
• Diagonal ruang: Ruas garis yang menghubungkan dua buah titik sudut pada prisma yang tidak terletak pada satu sisi atau bidang. Ada 4 diagonal ruang dalam prisma belah ketupat.
• Bidang diagonal: Bidang yang dibuat melalui diagonal sisi alas yang sejajar. Prisma belah ketupat memiliki 6 bidang diagonal.

Demikian pembahasan mengenai rumus volume dan luas permukaan prisma belah ketupat.