Rumus Volume Tabung dan Contoh Soalnya
Tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk dari dua buah lingkaran di bagian atas dan bawah. Ada juga persegi panjang yang mengelilingi kedua lingkaran tersebut. Tabung memiliki tiga sisi dan dua rusuk.
Tabung memiliki ciri-ciri kedua sisi berbentuk lingkaran, sementara satu sisinya persegi panjang yang melengkung. Dalam rumus Matematika, ada cara menghitung volume tabung. Volume tabung ini memudahkan menghitung suatu zat dalam tabung.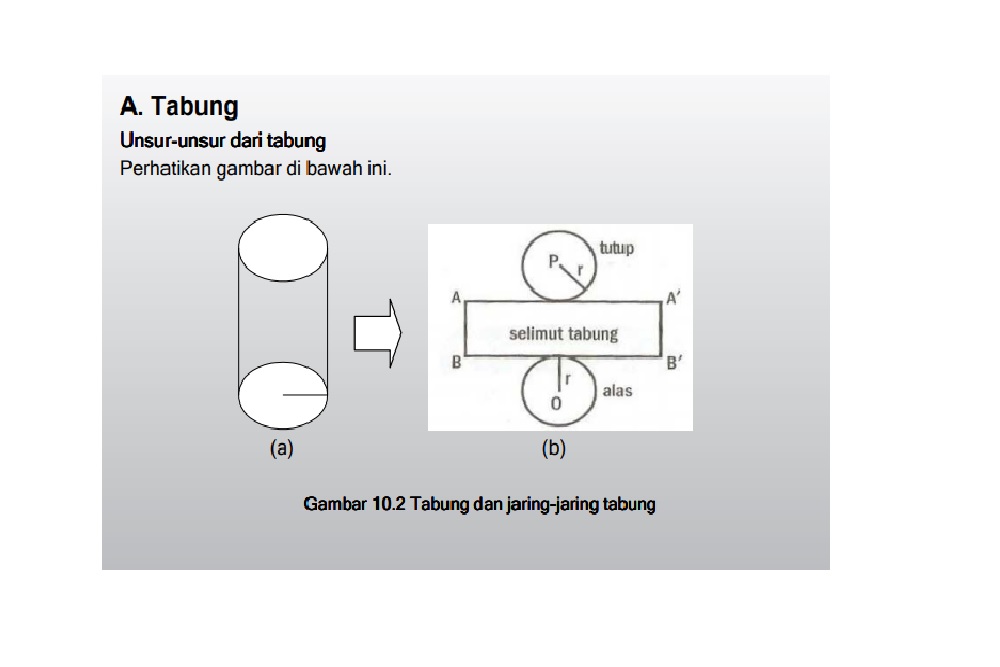
Rumus Volume Tabung
Volume adalah perhitungan dari banyaknya ruang atau kapasitas suatu benda yang dapat ditempati suatu objek. Volume tabung merupakan perkalian luas tabung dengan tinggi tabung. Mencari volume tabung dapat menghitung banyak ruang atau kapasitas tabung.
V = π x r x r x t
Atau
V = πr2t
Satuan Volume Tabung:
V= volume tabung (m³)
π= phi (3,14 atau 22/7)
r= jari-jari tabung (m)
t= tinggi tabung (m)
Rumus Mencari Volume Tabung
Cara mencari rumus volume tabung bisa dilakukan dengan percobaan sederhana. Pertama kumpulkan uang koin sebanyak Rp 500 sebanyak 36 buah. Kemudian lakukan cara berikut:
1. Ambil salah satu koin lalu ukur diameter. Hitung luas permukaan koin itu.
2. Tumpuk uang koin sebanyak 6 tumpukan, 8 tumpukan, 10 tumpukan dan 12 tumpukan.
3. Dari point kedua tersebut, Anda dapat memperkirakan volume tabung yang terbentuk dari tumpukan uang koin.
Misalnya, luas permukaan uang koin 7 centimeter persegi, dan banyaknya uang yang ditumpuk setara dengan tinggi tabung.
Berdasarkan penjelasan di atas volume tabung yaitu:
- Tumpukan pertama sebanyak 6 koin
V = 7 x 6 = 42 cm³
- Tumpukan kedua sebanyak 8 koin
V = 7 x 8 = 56 cm³
- Tumpukan ketiga 10 koin
V = 7 x 10 = 70 cm³
- Tumpukan keempat 12 koin
V = 7 x 12 = 84 cm³
Dari definisi volume tabung, rumus volume tabung diperoleh percobaan:
V = Luas permukaan tabung (lingkaran) x banyaknya tumpukan
V = π x r x r x t
Contoh Soal Volume Tabung
Berikut contoh soal volume tabung dari ebook Matematika Edisi Banguan Ruang Sisi Lengkung, ditulis Sufri dan Feri Tiona Pasaribu:
1. Gita memiliki kaleng bekas tempat susu bubuk berukuran cukup besar dan berbentuk tabung. Gita tidak ingin membuang kaleng tersebut. Akhirnya Gita membersihkan kaleng susu tersebut dan ingin digunakan sebagai tempat sirup. Adapun diameter dan tinggi kaleng tersebut masing-masing 20 cm dan 21 cm. Maka berapa liter sirup yang dapat ditampung oleh kaleng tersebut?
Catatan: 1 dm3 = 1 liter, π = 3,14 atau 22/7
Jawab:
Langkah 1: rumuskan dahulu penjabaran dari soal
Diameter kaleng (d)= 20 cm
Jari-jari kaleng (r)= setengah dari diameter (d)= 20:2= 10
Tinggi kaleng (t)= 21 cm
Langkah 2: menuliskan pertanyaan soal
Ditanya: Berapa liter sirup yang dapat ditampung oleh kaleng tersebut?
Langkah 3:
Menentukan liter sirup yang dapat ditampung kaleng memakai rumus volume tabung, sehingga:
V = π x r x r x t
V = 22/7 x 10 x 10 x 21
V = 22/7 x 100 x 21
V = 6.600
V = 6.600 dm³
V = 6.600 liter
(Diketahui 1000 cm3 = 1 dm³)
(1 dm3 = 1 liter)
Jadi, sirup yang dapat ditampung oleh kaleng susu tersebut sebanyak 6,600 liter
2. Di rumah Sari terdapat tangki air berbentuk tabung yang biasa digunakan untuk menampung air. Diameter dan tinggi masing-masing adalah 1 meter dan 1,5 meter. Pada suatu hari air di rumah Sari mati dan terpaksa keluarga Sari memakai air cadangan yang terdapat pada tangki tersebut yang sudah terisi penuh. Jika keluarga Sari menggunakan air sebanyak 1/3 tangki, maka berapa liter sisa air pada tangki?
Diketahui:
Diameter tangki (d) = 1 meter
Jari-jari tangki (r) = setengah diameter (d) = 1:2 = 0,5 meter
Tinggi tangki (t) = 1,5 meter
Pertanyaan:
Berapa sisa air yang teradapat pada tangki jika telah digunakan sebanyak 1/3 dari tangki?
Jawab:
Sisa air pada tangki yaitu
V = π x r x r x t
V = 3,14 x 0,5 x 0,5 x 1,5
V = 3,14 x 0,25 x 1,5
V = 1,1775 m³
V = 1.177,5 dm³
V = 1.177,5 liter
Karena air pada tangki sudah digunakan 1/3 dari tangki, maka 1/3 tangki adalah, 1.177,5 liter x 1/3 = 392,5 liter. Sehingga sisa air adalah 1.177,5 liter - 392,5 liter = 785 liter
Unsur Tabung
Tabung memiliki tiga unsur yang terdiri dari sisi tabung, selimut tabung, dan diameter. Berikut penjelasannya:
1. Sisi tabung
Merupakan bidang yang membentuk tabung. Sisi tabung ini terdiri dari selimut tabung dan dua buah lingkaran di atas tabung.
2. Selimut Tabung
Selimut tabung adalah bagian yang menutupi bentuk tabung. Persegi panjang dibentuk lingkaran yang disebut selimut tabung.
3. Diameter
Alas dan tutup tabung berbentuk lingkaran. Diameter lingkaran ini dipotong di bagian tengah. Sehingga muncul ukuran yang sama antara jarak potongan yaitu diameter tabung. Dari diameter tersebut, terdapat jari-jari yang ukurannya setengah dari diameter tabung.





