Cara Menghitung Luas Permukaan Tabung Beserta Contoh Soalnya
Luas permukaan tabung adalah salah satu hal yang dipelajari dalam pembahasan bangun ruang dan geometri. Sebab, tabung merupakan salah satu jenis bangun ruang sisi lengkung.
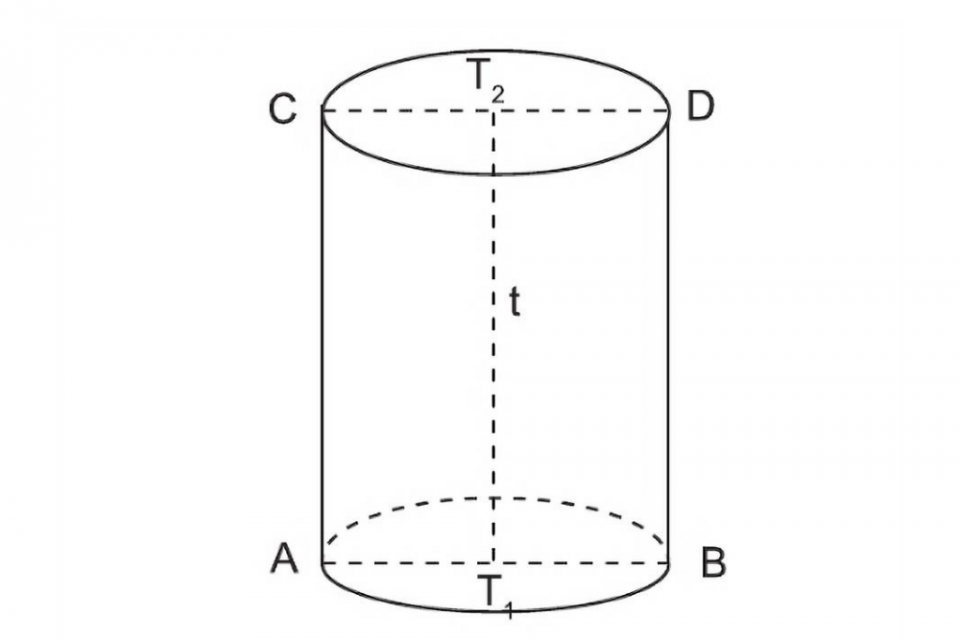
Tabung adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut.
Secara umum, tabung memiliki tiga bidang sisi utama yang terdiri dari bidang sisi alas atau alas tabung, bidang lengkung atau selimut tabung, dan juga bidang atas atau tutup tabung.
Adapun unsur-unsur tabung terdiri atas jari-jari dan diameter yang terdapat pada bagian alas atau tutup tabung, serta tinggi tabung yang merupakan jarak antara alas dan juga tutup tabung.
Ciri-Ciri Tabung
Dalam kehidupan sehari-hari, tabung digunakan dalam berbagai macam manfaat. Hal itu sering ditemukan di dapur dan terowongan jalan hingga tabung gas yang sering digunakan masak. Untuk mengetahui lebih dalam, kenali ciri-ciri tabung sebagai berikut:
- Memiliki 2 rusuk
- Memiliki 3 sisi, yaitu alas, selimut, dan tutup
- Memiliki 2 sisi berbentuk lingkaran
- Memiliki sisi berbentuk persegi panjang
- Sisi alas dan penutup memiliki ukuran yang sama besar dan saling berhadapan
- Tinggi tabung merupakan jarak antara alas dengan tutup
- Tidak memiliki diagonal bidang
- Tidak memiliki diagonal ruang
Rumus Luas Permukaan Tabung
Dalam buku Kapita Selekta Pembelajaran Geometri Datar Kelas VII, permukaan tabung adalah permukaan yang dilacak oleh sebuah garis yang disebut generatrix yang sejajar dengan dirinya sendiri dan selalu melewati bidang directrix yang tidak sejajar. Posisi tertentu dari matrik generatrix adalah elemen permukaan tabung.
Luas permukaan tabung sendiri merupakan hasil dari penjumlahan luas alas tabung + luas selimut tabung + luas tutup tabung.
- Rumus luas tutup tabung: 2πr
- Rumus luas alas tabung: 2πr
- Rumus luas selimut tabung: 2πr²t
Untuk menghitung keseluruhan dari luas permukaan sebuah tabung, rumus yang digunakan adalah sebagai berikut:
- L = 2 π r (r + t)
Rumus Luas Permukaan Tabung Tanpa Tutup
Luas permukaan tabung tanpa tutup memiliki rumus yang berbeda dari luas permukaan tabung. Karena tidak memiliki tutup, maka luas sisi tutup tabung yang berupa lingkaran tersebut tidak dihitung.
- Rumus luas tutup tabung: 2πr
- Rumus luas alas tabung: 2πr
- Rumus luas selimut tabung: 2πr²t
Untuk menghitung keseluruhan dari luas permukaan sebuah tabung tanpa tutup, rumus yang digunakan adalah sebagai berikut:
- L = (π x r2) + (2π r x t)
Keterangan:
L= Luas permukaan tabung
π = 22/7 atau 3,14
r = Jari – jari /setengah diameter (cm)
t = Tinggi (cm)
Contoh Soal dan Pembahasan
Untuk memahami rumus di atas, berikut ini terdapat beberapa contoh soal dan pembahasannya yang dapat Anda coba untuk latihan di rumah.
- Untuk membuat sebuah patung, pengrajin menggunakan sebuah batang pohon yang berbentuk seperti tabung dengan diameter 14 cm dan tinggi 18 cm. Tentukan luas permukaan dari batang kayu tersebut.
Penyelesaian:
Diketahui:
d= 14 cm
r = ½ x diameter = 7 cm
t = 18 cm
Ditanya: berapa luas permukaan batang kayu?
Jawab:
Luas permukaan = 2 π r (r + t)
Luas permukaan = 2 x 22/7 x 7 (7 + 18)
Luas permukaan = 44 x 25
Luas permukaan = 1.100 cm2
2. Diketahui sebuah kaleng minman berbentuk tabung. Diameternya 28 cm dan tingginya 40 cm. Tentukan luas permukaan kaleng tersebut?
Penyelesaian:
Diketahui:
d= 28 cm
r = ½ x diameter = 14 cm
t = 40 cm
Ditanya: berapa luas permukaan batang kayu?
Jawab:
Luas permukaan = 2 π r (r + t)
Luas permukaan = 2 x 22/7x 14 (14 + 40)
Luas permukaan = 88 x 54
Luas permukaan =4.752 cm2
3. Diketahui sebuah tabung tanpa tutup memiliki diameter sebesar 14 cm dan tinggi 35 cm. Berapakah luas permukaan tabung tersebut?
Penyelesaian:
Diketahui:
d= 14 cm
r = ½ x diameter = 7 cm
t = 35 cm
Ditanya: berapa luas permukaan tabung tanpa tutup?
Jawab:
Luas permukaan = (π x r2) + (2π r x t)
Luas permukaan = (22/7 x 7 x 7) + (2 x 22/7 x 7 x 35)
Luas permukaan = 154 cm2 + 1.540 cm2
Luas permukaan = 1.694 cm2
Demikianlah rumus permukaan tabung dengan tutup dan tanpa tutup. Soal dan pembahasan ini bisa digunakan sebagai bahan diskusi antara guru dan siswa di kelas.





