Memahami Rumus Refleksi dan Contoh Soal sebagai Bahan Belajar

Ketika mempelajari matematika, siswa diharuskan mempelajari transformasi geometri. Ini merupakan materi yang mempelajari tentang perubahan posisi dan ukuran suatu benda atau objek pada bidang geometri seperti garis, titik, maupun kurva.

Transformasi geometri sendiri dibagi menjadi empat jenis, yaitu translasi, rotasi, dilatasi, dan refleksi. 

Melansir laman Quipper Blog, refleksi atau pencerminan adalah perpindahan titik suatu objek pada bidang sesuai dengan sifat pembentukan bayangan pada cermin datar.

Pada prinsipnya, refleksi hampir sama dengan translasi, yaitu pergeseran. Hanya saja, pada refleksi memiliki sifat-sifat tertentu sedemikian sehingga posisi akhir objeknya merupakan hasil pencerminan objek awalnya.

Dalam praktiknya, terdapat rumus yang harus dihafalkan siswa ketika mempelajari refleksi. Lantas, apa rumus yang digunakan dalam materi ini? Simak pembahasannya di bawah ini.

Rumus Refleksi

Dalam mempelajari rumus refleksi, perlu Anda ketahui bahwa rumus refleksi ini digunakan berdasarkan refleksi atau pencerminan yang terjadi terhadap beberapa sumbu tertentu. Untuk lebih jelasnya, simak pembahasan lengkapnya di bawah ini.

1. Refleksi Terhadap Sumbu X dan Sumbu Y

Rumus refleksi ini berlaku jika refleksi terjadi terhadap sumbu X dan sumbu Y. 

Anda harus mengingat konsep dari pencerminan, yaitu jarak objek ke cermin = jarak bayangan ke cermin. 

Jika cermin diibaratkan sebagai sumbu X, maka rumus refleksi Matematika terhadap sumbu X adalah sebagai berikut:

(x, y) → (x, -y)

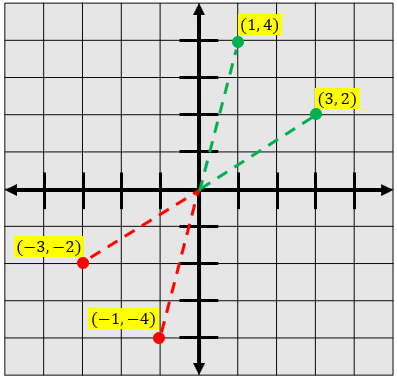
Contohnya, jika Anda memiliki titik potong yang berada di (3, 2), refleksi terhadap sumbu X dari titik potong tersebut dapat dilihat pada gambar di bawah ini:

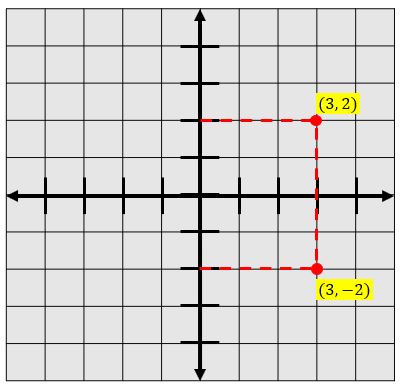
Lalu, bagaimana jika cermin diibaratkan sebagai sumbu Y atau refleksi terhadap sumbu Y? 

Rumus refleksi Matematika terhadap sumbu Y adalah sebagai berikut:

(x, y) → (-x, y)

Contohnya, jika Anda memiliki titik potong yang berada di (3, 2), refleksi terhadap sumbu Y dari titik potong tersebut dapat dilihat pada gambar di bawah ini:

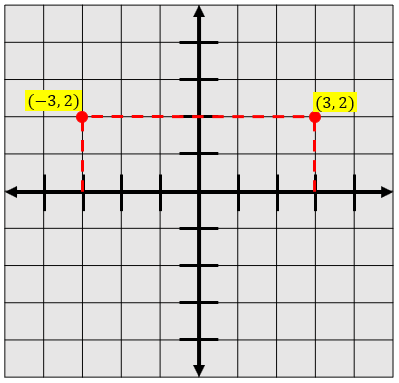
2. Refleksi Terhadap Garis Y = X dan Y = -X

Pada garis Y = X dan Y = -X, rumus refleksi Matematikanya adalah berikut:

(x, y) → (xˡ, yˡ)

Dengan keterangan:

• xˡ = y dan yˡ = x pada garis Y = X
• xˡ = -y dan yˡ = -x pada garis Y = -X

Jadi, jika Anda memiliki titik potong (4, 2), refleksi terhadap garis Y = X dan Y = -X adalah seperti dalam gambar berikut:

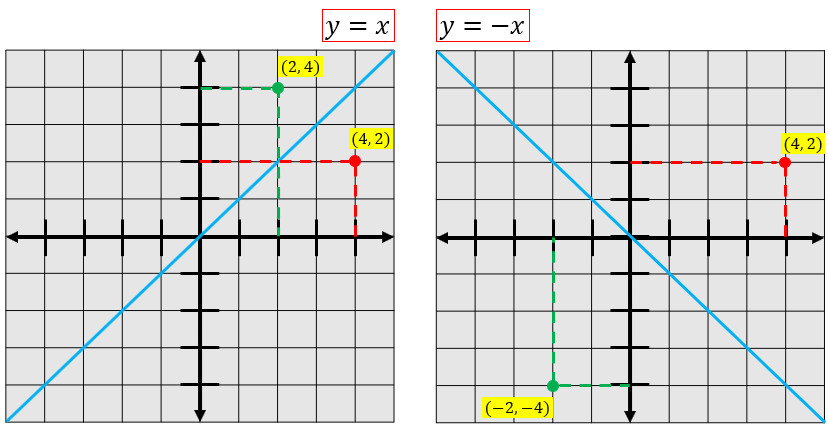
3. Refleksi Terhadap Garis X = H dan Y = K

Untuk memahami refleksi Matematika terhadap garis X = H dan Y = K, Anda harus terlebih dahulu memahami konsep cermin dan konsep refleksi terhadap sumbu X dan sumbu Y.

Adapun rumus refleksi yang digunakan yaitu:

• Refleksi terhadap garis X = H

(x, y) → (2H – x, y)

• Refleksi terhadap garis Y = K

(x, y) → (x, 2K – y)

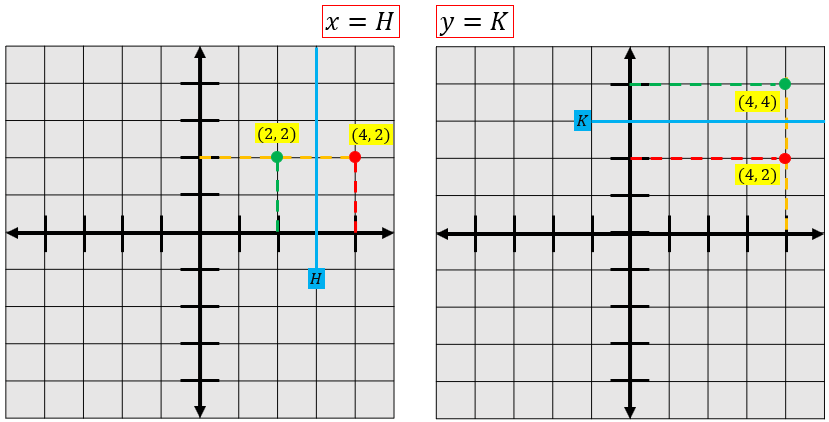
Untuk X = H, misalnya Anda memiliki titik seperti pada di gambar. Koordinat y akan selalu sama dan yang berubah adalah koordinat x. 

Bagaimana cara mengetahui jarak dari H ke titik tersebut? Jarak tersebut dapat diketahui dengan cara jarak H dikurangi jarak titik tersebut.

H – X adalah 3 – 2 = 1.

Setelah mengetahui jarak antara H dan X, Anda dapat menentukan di mana letak Xˡ dengan cara menambah H dengan hasil operasi sebelumnya atau Xˡ = H + (H – X). Bentuknya juga dapat diubah menjadi Xˡ = 2H – X.

Jadi, 2H – X = 2(3) – 2 = 6 – 2 = 4,

maka Xˡ = 4.

Untuk Y = K, misalnya Anda memiliki titik seperti pada di gambar. Kebalikan dari sebelumnya, koordinat x akan selalu sama dan yang berubah adalah koordinat y. Cara menghitungnya pun sama. 

Jarak K dan Y dapat diketahui dengan cara jarak H dikurangi jarak titik tersebut.

K – Y adalah 3 – 2 = 1.

Kemudian, letak Yˡ dapat ditentukan dengan cara

Yˡ = K + (K – X) atau Yˡ = 2K – Y.

Jadi, 2K – Y = 2(3) – 2 = 6 – 2 = 4,

maka Yˡ = 4.

4. Refleksi Terhadap Titik Asal 0 (0, 0)

Terakhir, ada  rumus refleksi terhadap titik asal 0 atau (0, 0). Adapun rumus yang digunakan yaitu:

(x, y) → (-x, -y)

Perhatikan gambar di bawah ini:

Contoh Soal Refleksi

Berikut ini lima contoh soal tentang refleksi dari berbagai sumber yang bisa dipelajari agar paham penerapan rumusnya yang baik dan benar. 

Contoh Soal 1

Tentukan bayangan/refleksi titik A(6,-3) oleh pencerminan terhadap sumbu x.

 

Jawaban:

 

P pencerminan terhadap sumbu x.

 

P: (x,y) -> (x,-y) akibatnya bayangan dari A(6,-3) -> A’(6,3)

 

B(5,7) -> B’(5,-7)

Contoh Soal 2

Tentukan bayangan segitiga STU dengan S(-2,4), T(3,-7), U(6,5) oleh pencerminan terhadap sumbu y=-x.

 

Jawaban:

 

Bayangan STU oleh s pencerminan terhadap sumbu y = -x adalah (x,y) -> (-y.-x)

 

S(-2,4) -> (-4,2)

 

S(3,-7) -> (7,-3)

 

S(6,5) -> (-5,-6)

 

Contoh Soal 3

Tentukan bayangan dari setiap titik pada pencerminan titik (3,-5) oleh pencerminan terhadap sumbu-x.

 

Jawab:

 

 

Dengan menggunakan perkalian matriks, x' dan y' ditentukan sebagai berikut:

 

 

Jadi, bayangan titik P(3,-5) oleh pencerminan terhadap sumbu-x adalah titik P'(3,5).

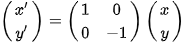
Contoh Soal 4

Tentukan bayangan dari setiap titik pada pencerminan titik (-1,-3) oleh pencerminan terhadap garis y = x.

 

Jawab:

 

 

Dengan menggunakan perkalian matriks, x' dan y' ditentukan sebagai berikut:

 

 

Jadi, bayangan titik P(-1,-3) oleh pencerminan terhadap garis y = x adalah titik P'(-3, -1).

Contoh Soal 5

Tentukan bayangan dari (2, -4) oleh refleksi berurutan terhadap x = 3, kemudian x = 7.

 

Jawaban:

 

(M2x . M1x)(x,y) = (2(b-a) + x,y)

 

Pada soal ini, a = 3, b = 7, sehingga:

 

(M2x . M1x)(2, -4) = (2(7-3) + 2, -4)

 

= (-6, -4)

 

Itulah rangkuman informasi mengenai rumus refleksi beserta contoh soalnya yang bisa dipelajari sebagai bahan belajar.