Pengertian, Jenis, dan Contoh Soal Vektor Matematika

Pada matematika SMA, siswa akan mempelajari berbagai materi. Salah satunya materi vektor matematika dimana siswa akan mempelajari besaran yang mempunyai nilai besar dan arah.
Dalam kehidupan sehari-hari, ilmu matematika ini diterapkan dalam pembuatan grafis di software komputer dan GPS atau map. Bahkan, vektor juga banyak digunakan dalam bidang militer, teknik sipil, navigasi, dan lainnya.
Agar lebih paham tentang materi ini, berikut di bawah ini penjelasan lengkapnya mulai dari pengertian hingga contoh soal dan pembahasannya yang bisa dipelajari.
Pengertian Vektor Matematika
Berdasarkan penjelasan dari emodul Kemdikbud Matematika Peminatan Kelas 10 karya Entis Sutisna, vektor merupakan besaran yang memiliki arah dan besar, yang umumnya dinyatakan dengan ruas garis berarah.
Dalam konsep matematika, vektor merupakan ruas garis berarah yang panjangnya adalah jarak dari titik pangkal ke titik ujung. Sementara arahnya yaitu arah dari pangkal ke ujung atau perpanjangannya.
Oleh karena itulah, vektor dilambangkan dengan tanda panah (→). Besar vektor dinyatakan oleh panjang ruas garis berarah, sedangkan arah vektor dinyatakan dari kemiringan ruas garis dan anak panahnya.
Dalam matematika, vektor bisa disajikan secara geometris dan aljabar. Vektor bisa dinyatakan sebagai segmen garis berarah, yang panjang segmennya menyatakan besar vektor, dan arah anak panah menyatakan arah vektor.

Foto: dok. Modul Kemdikbud Matematika Peminatan Kelas 10 oleh Entis Sutisna
Pada bidang koordinat, vektor yang digambarkan akan mempunyai komponen horisontal (gerakan ke kanan/kiri dan sejajar sumbu X) dan komponen vertikal (gerakan ke atas/bawah atau sejajar sumbu Y).
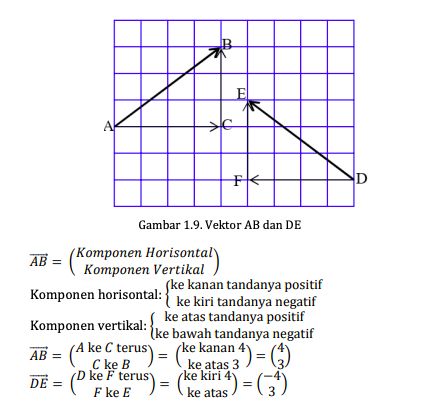
Foto: dok. Modul Kemdikbud Matematika Peminatan Kelas 10 oleh Entis Sutisna
Apabila diberikan komponen-komponen suatu vektor, vektor tersebut bisa digambar dan dapat ditentukan besarnya.
Jenis-jenis Vektor Matematika
1. Vektor Nol
2. Vektor Posisi
3. Vektor Satuan
4. Vektor Basis
Rumus Vektor Matematika
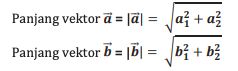
Foto: dok. Modul Kemdikbud Matematika Peminatan Kelas 10 oleh Entis Sutisna
Contoh Soal Vektor Matematika dan Pembahasannya
Berikut ini sepuluh contoh soal vektor matematika serta pembahasannya yang bisa dipelajari agar lebih paham tentang materi ini.
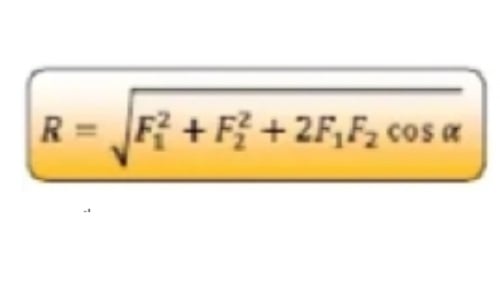
1. Dua buah vektor masing masing F1 = 15 satuan dan F2 = 10 satuan. Mengapit sudut sebesar 60°. Tentukan besaran resultan vektor!
Pembahasan contoh soal vektor
Diketahui:
F1 = 15
F2 = 10
α = 60°
R = ….?
Sehingga
R = √15² + 10² + 2 . 15 . 10 . (0,5)
= √225 + 100 + 150 = √475
= √ 25.19
= 5 √19 satuan
2. Dua buah vektor gaya masing-masing 8N dan 4N saling mengapit sudut 120°. Berapakah resultan kedua vektor tersebut?
Pembahasan
Diketahui :
F1 = 8N
F2 = 4N
α = 120°
R = …. ?
Sehingga
R = √8² + 4² + 2 . 8 . 4 . cos 120°
= √8² + 4² + 2 . 8 . 4 . (-0,5) = √64 + 16 - 32
= √48
= √16.3
= 4 √3 Newton
3. Dua buah vektor gaya yang sama sama besar masing-masing vektor besarnya adalah 10 Newton. Jika sudut yang terbentuk antara kedua vektor tersebut adalah 60°, tentukan besar nilai resultan vektor.
Jawaban:
Jawaban Contoh Soal Vektor
Diketahui:
F1 = 10 N
F2 = 10 N
α = 60°
Resultan vektor =... ?
Maka
R = √10² + 10²+ 10 . 10 cos 60°
R = √10² + 10²+ 10 . 10 . 0,5
R= √300
= 10√3 Newton
4. Dua buah vektor kecepatan A dan B masing-masing besarnya adalah 40 m/s dan 20 m/s. Yang membentuk sudut sebesar 60°. Tentukan selisih kedua vektor tersebut.

Pembahasan contoh soal vektor:
5. Sebuah mobil bergerak ke Utara sejauh 20 km. Kemudian bergerak ke Barat sejauh 40 km. Selanjutnya bergerak ke selatan sejauh 10 km. Tentukan besaran perpindahan mobil tersebut!
Pembahasan:
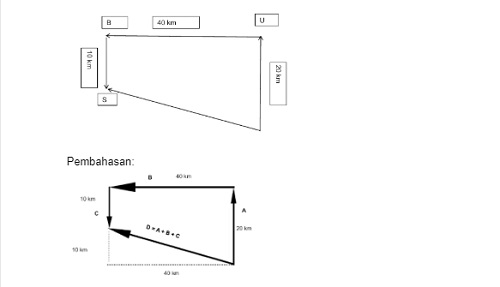
Jika perpindahan pertama dinyatakan vektor A, perpindahan kedua vektor B, dan perpindahan ketiga vektor C, maka perpindahan total dinyatakan vektor D.
Maka :
√40² + 10² = 10√17 m
Perkalian vektor A dengan skalar 2: 2A = 2(3, 5) = (6, 10).
Itulah rangkuman mengenai vektor matematika mulai dari pengertian hingga contoh soal dan pembahasannya yang bisa dipelajari.





