Pengertian Bilangan Prima: Contoh, Cara Menentukan, dan Manfaat
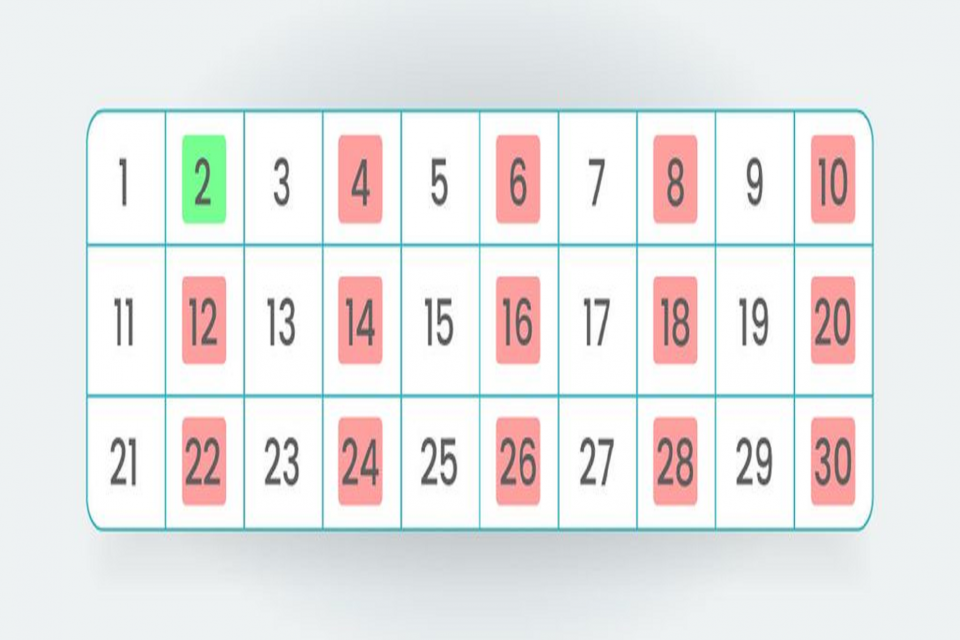
Apa itu bilangan prima? Bilangan prima adalah bilangan bulat lebih dari satu yang hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Contoh bilangan prima yaitu 2, kenapa tidak 1? Sebab angka satu hanya bisa dibagi dengan dirinya sendiri, sedangkan bilangan prima memiliki dua faktor.
Bilangan atau angka prima sudah ditemukan sejak zaman Yunani Kuno oleh ilmuwan Euclid dari Alexandria. Bilangan ini ditemukan pada catatan berusia 300 tahun Sebelum Masehi (SM). Euclid menyampaikan bahwa banyaknya bilangan prima tidak terbatas.
Bilangan Prima adalah?
Bilangan prima adalah bilangan asli lebih dari 1 yang hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Apakah bilangan ganjil termasuk bilangan prima? Jawabannya tidak, karena ada bilangan ganjil yang dapat dibagi bilangan lain selain 1 dan bilangan itu sendiri. Bilangan ganjil misalnya angka 9 yang dapat dibagi 1, 9 dan 3.
Bilangan prima tidak dapat dibagi habis oleh bilangan bulat lain selain dirinya sendiri. Contohnya bilangan 2,3,5,7 dan 11 karena faktor-faktor pembaginya hanya 1 dan bilangan itu sendiri.
Sejarah Singkat Bilangan Prima
Sejarah singkat bilangan prima sudah dikenal sejak zaman Yunani kuno, di mana para matematikawan dari zaman Yunani, seperti Eratosthenes dan Euclid mulai mempelajari sifat-sifat yang dimiliki bilangan prima. Bahkan Euclid mengajarkan algoritma untuk menemukan bilangan prima dalam karya terkenalnya, yaitu Elemen.
Para ilmuwan Arab dan Persia, seperti Al-Farisi, Al-Khawarizmi, dan Al-Kashi juga mempelajari bilangan prima dan menemukan metode untuk menemukan bilangan prima yang besar. Pada era modern, bilangan prima menjadi penting dalam kriptografi dan keamanan informasi, karena kunci enkripsi kuat bisa dibangun dengan memanfaatkan sifat bilangan prima. Tidak hanya itu, bilangan prima menjadi subjek penelitian dalam beragam cabang Matematika, seperti teori graf, teori bilangan dan teori kompleksitas.
Cara Menentukan Bilangan Prima
Ada banyak cara yang dapat digunakan untuk menentukan apakah bilangan dapat disebut sebagai bilangan prima atau tidak. Berikut cara menentukan bilangan prima dalam Matematika:
1. Cek apakah bilangan itu lebih besar dari 1 atau tidak, karena bilangan prima harus lebih besar dari angka 1.
2. Cek apakah bilang ini bisa habis dibagi oleh bilangan selain 1 dan dirinya sendiri. Bilangan prima hanya habis dibagi bilangan itu sendiri.
Contoh Bilangan Prima 1-1000
Berikut contoh bilangan prima antara 1-1000:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 293, 307, 311, 313, 317, 331, 337, 347, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, dan 997.
Manfaat Bilangan Prima
Meski banyak orang tidak menyukai materi bilangan prima, ada banyak manfaat yang bisa diperoleh dari bilangan prima. Berikut di antaranya:
1. Memperdalam Ilmu Matematika
Bilangan prima merupakan salah satu ilmu Matematika yang menarik dan unik. Mempelajari bilangan prima membantu dalam memahami konsep Matematika.
2. Kriptografi
Bilangan prima juga diperlukan dalam kriptografi, yaitu ilmu yang berkaitan dengan penyandian pesan. Contohnya algoritma RSA yang menggunakan bilangan prima untuk menghasilkan kunci penyandian.
3. Menstimulasi Otak
Mempelajari bilangan prima dan terus berlatih dapat membantu meningkatkan kemampuan berpikir secara analitis dan logis. Selain itu, dapat meningkatkan daya ingat manusia.
4. Pemograman
Bilangan prima juga banyak digunakan dalam algoritma dan program komputer. Contohnya dalam menyelesaikan masalah, seperti mencari faktor dari sebuah bilangan atau optimasi program.
5. Ilmu Pengetahuan Lainnya
Tidak hanya dalam pelajaran Matematika, bilangan prima juga dapat digunakan untuk beragam bidang ilmu pengetahuan lainnya. Di antaranya biologi, ekonomi dan fisika.
Dapat disimpulkan bilangan prima adalah bilangan yang memiliki dua faktor, dibagi oleh bilangan itu sendiri dan bilangan lain selain 1. Bilangan prima ini dimanfaatkan untuk memperdalam ilmu Matematika, kriptografi, menstimulasi otak, pemograman dan ilmu pengetahuan lainnya.






