Memahami Rumus Luas Selimut Kerucut Beserta Contoh Soalnya
Dalam mempelajari matematika, salah satu hal yang wajib dipahami adalah terkait rumus luas selimut kerucut. Pasalnya, pelajaran ini menjadi salah satu syarat lulus dari mata pelajaran Matematika.
Sebelum membahas langsung terkait rumus luas selimut kerucut, pada umumnya siswa akan dijelaskan terlebih dahulu terdapat dua jenis bangun yakni bangun datar dan bangun ruang. Bangun kerucut merupakan bangun ruang karena memiliki ruang di dalamnya.
Rumus luas selimut kerucut sebenarnya mudah dipahami. Cukup ikuti beberapa rumus dan dapat diterapkan dalam berbagai soal di bawah ini. Selain itu, pahami pula unsur-unsur kerucut beserta ciri-ciri kerucut.
Selimut kerucut yakni sisi atau bidang yang melengkung melingkari alasnya. Agar lebih mudah memahaminya, simak ulasan berikut.
Unsur-unsur Kerucut
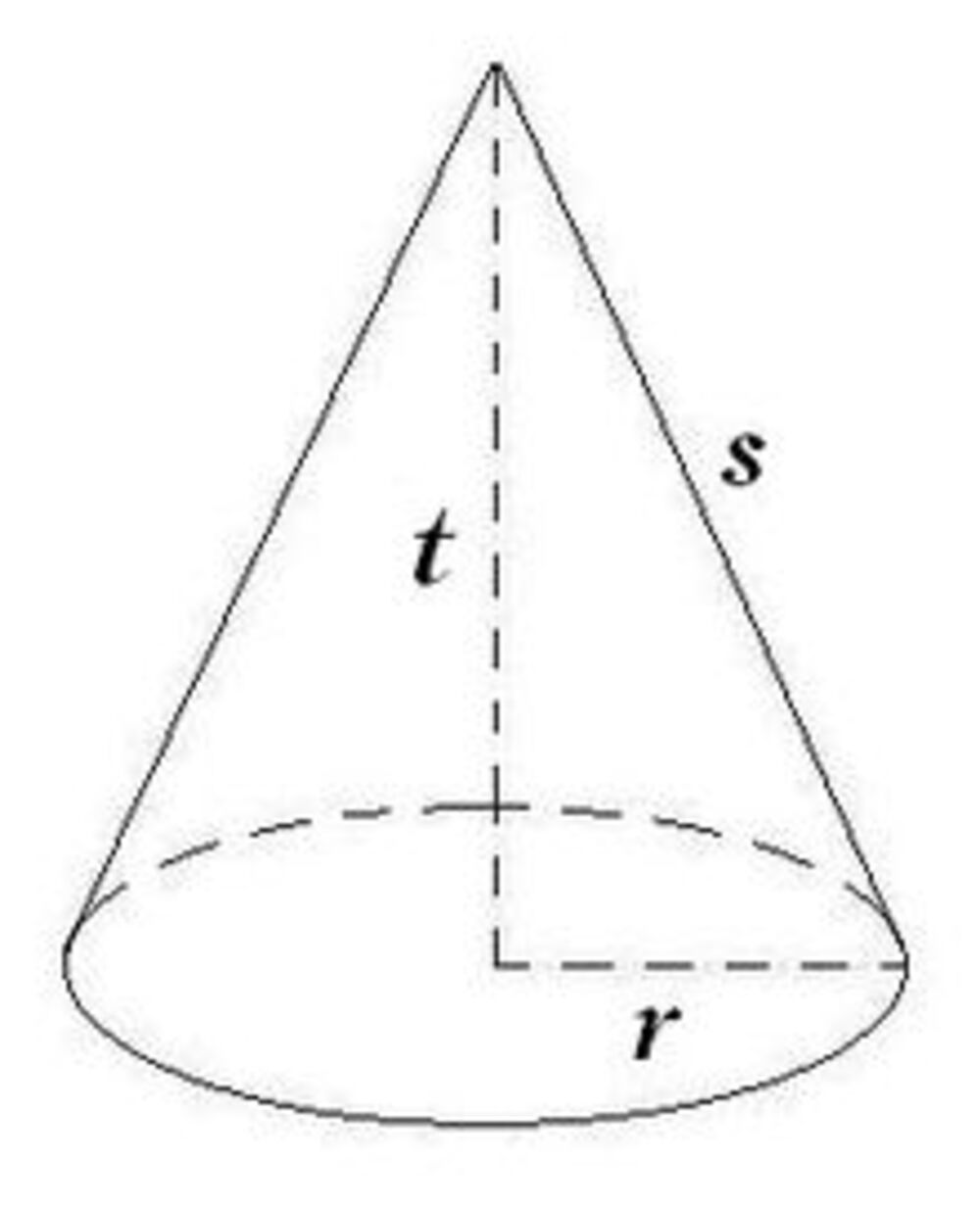
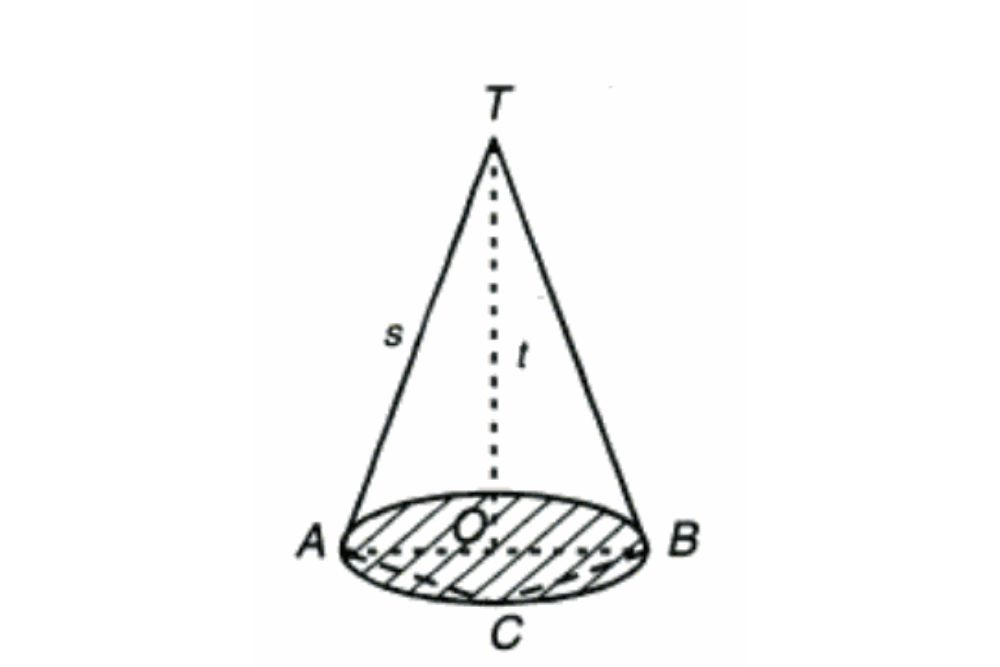
Kerucut adalah sebuah bangun ruang dengan satu titik sudut dan dua sis. Sebelum menilik rumus luas selimut kerucut, perlu memahami terlebih dahulu unsur-unsur kerucut. Unsur-unsur kerucut meliputi:
- Sisi yang ada di bawah dinamakan bidang alas kerucut.
- Lingkaran atau O di bawah dinamakan pusat lingkaran (pusat bidang alas kerucut) sedangkan titik ujung lainnya di bagian atas dinamakan puncak kerucut.
- Ruang di antara titik tengah lingkaran alas kerucut ke garis lingkaran luar dinamakan jari-jari bidang alas kerucut.
- Ada pula bagian yang dinamakan diameter bidang alas kerucut.
- Ruas garis yang menghubungkan titik ujung dan alas lingkaran tengah kerucut dinamakan tinggi kerucut.
- Ada pula tali busur bidang alas kerucut.
- Sisi yang tidak diarsir dinamakan selimut kerucut.
- Adapun ruas-ruas garis pada selimut kerucut yang menghubungkan titik puncak dan titik-titik pada lingkaran dinamakan garis pelukis kerucut.
Ciri-ciri Bangun Ruang Kerucut
Selanjutnya, ada pula ciri-ciri kerucut yang perlu dipahami. Berkaitan dengan itu, simak beberapa ciri-ciri berikut:
- Terdapat satu titik sudut yang fungsinya yakni puncak kerucut. Puncak kerucut terlihat pada bagian paling atas dan paling ujung.
- Terdapat dua sisi pada kerucut yakni sisi juring pada selimut dan lingkaran pada bagian alasnya.
- Terdapat satu buah rusuk yang mengelilingi alas berbentuk lingkaran. Sisi ini seakan menopang bangun sehingga membentuk segitiga jika dilihat dari satu sisi. Namun sesungguhnya sisi ini mengelilingi.
- Terdapat seperti dua garis tegak sebagai garis semu atau garis pelukis di bagian kanan dan kiri kerucut.
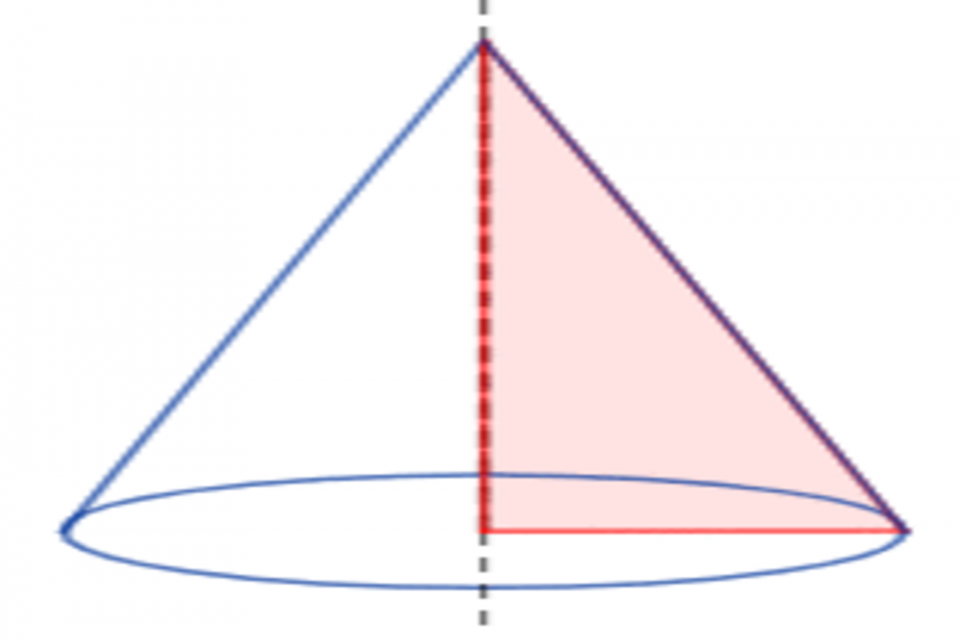
- Terdapat bentuk segitiga sama kaki atau segitiga siku-siku yang terlihat dari dua dimensi.
Rumus Luas Selimut Kerucut
Kerucut memiliki empat bagian atau sisi yang kerap muncul dalam perhitungan. Kerucut bentuknya mirip seperti cone ice cream, topi ulang tahun, dan lain sebagainya.
Seperti yang sudah dijelaskan, sisi tersebut adalah alas kerucut, tinggi kerucut, selimut kerucut, dan apotema atau garis pelukis. Selimut kerucut terlihat seperti segitiga, tetapi pada dasarnya bentuknya seperti juring lingkaran.
Selimut kerucut adalah permukaan melengkung yang membungkus kerucut. Oleh karena itulah untuk mencari luasnya cukup rumit.
Untuk memahami rumus luas selimut kerucut, berikut rumus luas selimut kerucut sebagai berikut:
π x r x s
Keterangan:
π = 3,14 atau 227
r = jari-jari
s = apotema atau garis pelukis
Contoh Soal dalam Penggunaan Rumus Luas Selimut Kerucut
Contoh Soal 1
Anna ingin membuat topi berbentuk kerucut dari kertas. Anna pun ingin membuat topi dengan diameter 24 cm dan tinggi 16cm. Jika demikian, berapa luas kertas yang dibutuhkan oleh Anna?
Jawab:
Diketahui:
Diameter = 24 cm, maka r = 24 : 2 = 12 cm
r = 12 dan t = 16 cm
Oleh karena itu, maka penghitungannya membutuhkan apotema dengan rumus apotema. Rumus apotema yakni sebagai berikut:
S= √r2+√t2
S= √122+√162
S= √144+√256
S= √400=20 cm
Selanjutnya, hitung dengan rumus luas permukaan dengan rumus sebagai berikut:
L = π x r x s
L = 3,14 x 12 x 20
L = 753,6 cm2
Berdasarkan penghitungan di atas, maka luas kertas koran yang diperlukan oleh Ria adalah 753,6cm2
Contoh Soal 2
Jari-jari alas kerucut adalah 6 cm. Tinggi kerucut adalah 8 cm. hitung luas selimut kerucut dan luas permukaan kerucut beserta cara menghitungnya.
Jawab:
Diketahui:
π = 3,14 (pi)
r = 6 cm (jari-jari)
t = 8 cm (tinggi)
Langkah pertama, perlu dicari terlebih dahulu panjang garis pelukis kerucut.
S (apotema) = √r2 + t2
= √62 + 82
= √100
= 10
Maka, luas selimut kerucut = πrs = 3,14 × 6 × 10 = 188,4. Jadi jawaban luas selimut kerucut adalah 188,4 cm2. Luas permukaan kerucut = luas selimut + luas alas = 188,4 + (πr2). Luas permukaan kerucut = 188,4 + (3,14 × 6 × 6) = 301,44. Kemudian, luas permukaan kerucut tersebut adalah 301,44 cm2.
Contoh Soal 3
Bangun kerucut memiliki luas selimut 353,25 cm² dan panjang jari-jari 7,5 cm. Hitung luas permukaan kerucut.
Diketahui:
Luas selimut = 353,25 cm²
r = 7,5 cm
Jawab:
L = luas selimut + luas alas
L = (π r s) + (π r²)
L = (353,25) + (3,14 x 7,5 x 7,5)
L = 353,25 + 176,625
L = 529,875 cm²
Sehingga, luas permukaan kerucut di atas adalah 529,875 cm².
Demikian rumus luas selimut kerucut yang muncul pada mata pelajaran matematika selengkapnya.