Persamaan Garis Singgung Lingkaran, Definisi, Rumus dan Contohnya

Persamaan garis singgung lingkaran merupakan salah satu materi dalam pelajaran Matematika. Berkenaan dengan itu, menarik untuk membahasnya lebih lanjut.
Materi tersebut berkaitan dengan bangun datar berupa lingkaran. Materi lingkaran tidak hanya berupa luas dan keliling, tetapi ada pula persamaan lingkaran dan garis singgung lingkaran.
Agar dapat lulus dari mata pelajaran tersebut, siswa pun wajib memahaminya. Untuk itu, berikut penjelasan lengkap terkait persamaan garis singgung lingkaran.
Pengertian Persamaan Garis Singgung Lingkaran
Garis singgung lingkaran adalah garis yang menyentuh lingkaran dan tepat di satu titik. Ketika lingkaran berdiri dan bersentuhan sisi bawahnya, maka titik sentuhan antara lingkaran terluar dengan permukaan bawahnya adalah garis singgung.
Contohnya yakni ketika ada roda sepeda motor yang berdiri berputar. Kemudian roda tersebut terkena permukaan jalan yang datar. Titik sentuhan antara roda sepeda motor dan jalan itulah yang disebut dengan garis singgung lingkaran. Contoh lainnya, yakni kertas berbentuk lingkaran yang ditempelkan batang lidi di atasnya.
Berdasarkan contoh itu, diketahui bahwa lidi adalah garis singgung lingkaran. Contoh di atas berupa jenis persamaan garis singgung lingkaran dari gradien.
Jenis Persamaan Garis Singgung Lingkaran
Terdapat tiga jenis persamaan garis singgung lingkaran yang wajib diketahui. Ketiganya dibedakan berdasarkan lokasi atau letak garis yang menyinggung lingkaran tersebut. Berikut penjelasannya:
1. Persamaan Garis Singgung Lingkaran Melalui Titik Pada Lingkaran
Persamaan garis singgung ini pada dasarnya seperti contoh sepeda di atas. Garis singgungnya berada tepat di sisi terluar sisi lingkaran. Letaknya tidak berjarak dan tidak masuk ke dalam lingkaran tersebut.
2. Persamaan Garis Singgung Lingkaran dari Gradien
Persamaan garis singgung jenis ini yakni ketika garis singgung berada di dalam lingkaran jika dilihat dari satu sisi. Terlihat garis tersebut berupa garis lurus yang seakan membelah lingkaran. Garis inilah yang membedakan persamaan garis singgung lingkaran gradien dan melalui titik.
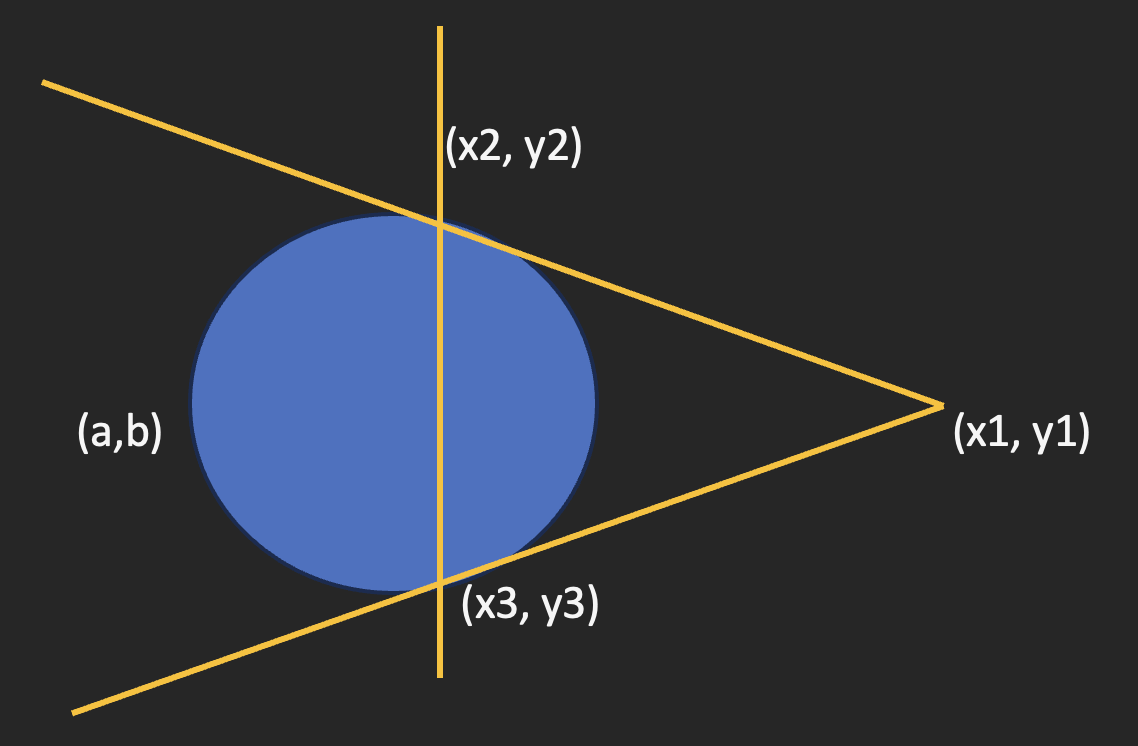
3. Persamaan Garis Singgung Lingkaran Melalui Titik di Luar Lingkaran
Garis singgung yang ada pada jenis ini terletak di titik di luar lingkaran. Artinya, garis itu tidak bersentuhan dengan sisi terluar lingkaran, melainkan menjauhinya.
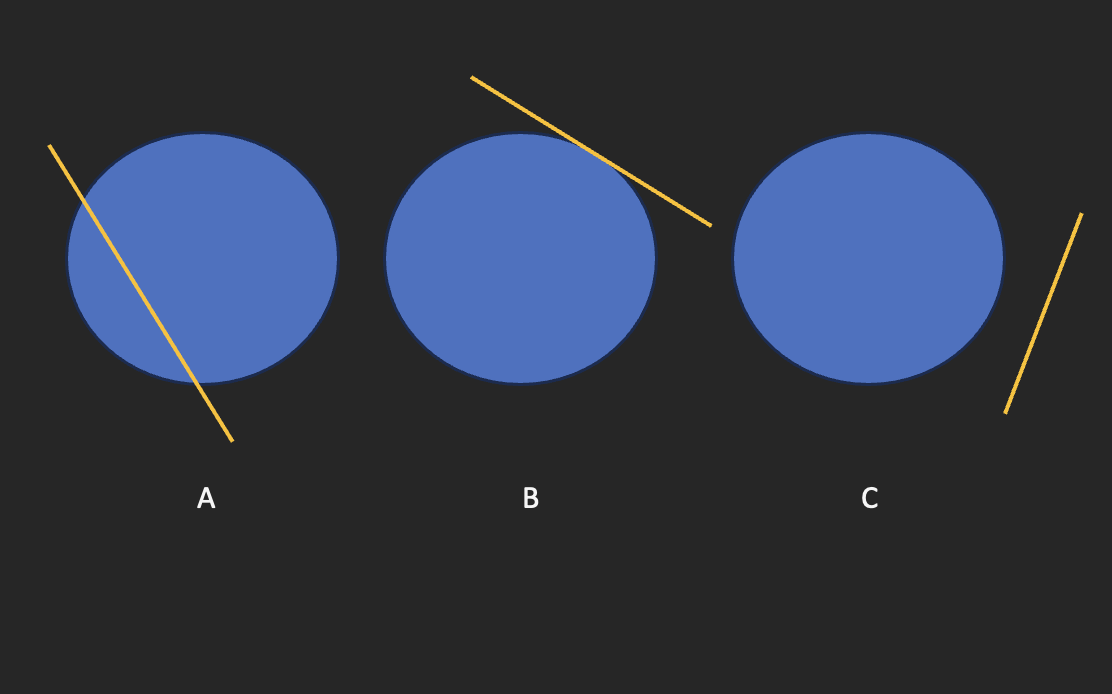
Keterangan Gambar:
A: Persamaan Garis Singgung Lingkaran dari Gradien
B: Persamaan Garis Singgung Lingkaran Melalui Titik Pada Lingkaran
C: Persamaan Garis Singgung Lingkaran Melalui Titik di Luar Lingkaran
Rumus Persamaan Garis Singgung Lingkaran
Setelah mengetahui pengertian dan macam persamaan garis singgung lingkaran, adapun rumus yang perlu dipahami oleh siswa. Rumus-rumus ini dibedakan berdasarkan macam persamaan garis singgung lingkaran di atas.
1. Rumus Persamaan Garis Singgung Lingkaran Melalui Titik Pada Lingkaran
| Persamaan Lingkaran | Persamaan Garis Singgung Lingkaran |
| X2 + y2 = r2 | Xx1 + yy1 = r2 |
| (x-a)2 + (y-b)2 = r2 | (x-a) (x1 – a) + (yb) = r2 |
| X2 + y2 + Ax + By + C = 0 | Xx1 + yy1 + ½ A (x+x1) + ½ B(y+y1) + C = 0 |
2. Rumus Persamaan Garis Singgung Lingkaran dari Gradien
| Persamaan Lingkaran | Persamaan Garis Singgung Lingkaran |
| X2 + y2 = r2 | Y = mx ± rÖ1 + m2 |
| (x-a)2 + (y-b)2 = r2 | Y – b = m (x-a) ± rÖ1+m2 |
3. Rumus Persamaan Garis Singgung Lingkaran Melalui Titik di Luar
• Pusat (0,0) : x1x + y1y = r2
• Pusat (a,b) : (x1– a ) ( x-a) + (y1– b) ( y-b ) = r2
• Bentuk Umum: x1x + y1y + ½ A (x1 + x) + ½ B (yq + y) + C = 0
Contoh Soal Persamaan Garis Singgung Lingkaran
Setelah membahasn pengertian, jenis dan rumus persamaan garis singgung lingkaran, menarik untuk menilik contoh soal terkait materi Matematika tersebut. Berikut ini contoh soal dan pembahasannya.
1. Contoh Soal Persamaan Garis Singgung Lingkaran 1
Gradien yang menyinggung lingkaran (x-1)2 + (y+1)2 = 25 di titik A (4,2) yakni?
Jawab:
( x-1) (x1– 1 ) + ( y+1 ) (y1+1) = 25
( x-1) (4- 1 ) + ( y+1 ) (2+1) = 25
3x + 3y = 25
y = -x + 25/3
Jawaban: gradien garis yang menyinggungnya adalah -1.
2. Contoh Soal Persamaan Garis Singgung Lingkaran 2
Persamaan garis yang menyinggung lingkaran x2 + y2 = 5 di titik A (2,1) yakni?
Jawab:
x1 = 2 dan y1 = 5
Persamaan garis singgung lingkaran xx1 + yy1 = r2
xx1 + yy1 = 5
Jawaban: 2x + y = 5
3. Contoh Soal Persamaan Garis Singgung Lingkaran 3
Persamaan garis singgung yang dengan gradien 2 dan menyinggung x2 + y2 = 5 yakni?
Jawab:
Diketahui persamaan garis singgungnya y = 2x + 5 dan y = 2x – 5.
Jawabannya adalah y = 2x + 5
4. Contoh Soal Persamaan Garis Singgung Lingkaran 4
Persamaan garis singgung pada titik (4, -1) pada lingkaran L = x² + y² + 6x - 4y - 45 = 0 adalah?
Jawab:
Diketahui titik (4, -1) pada lingkaran L = x² + y² + 6x - 4y - 45 = 0
Alasannya yakni 16 + 1 + 24 + 4 - 45 = 0.
Oleh karena itu, persamaan garis singgung di titik (4, -1) adalah:
(4)x + y(-1) + 3(x + 4) - 2(y - 1) - 45 = 0
7x - 3y - 31 = 0
Jawaban: 7x - 3y - 31 = 0
Itulah penjelasan mengenai pengertian, macam, rumus, dan contoh soal beserta pembahasannya dalam materi persamaan garis singgung lingkaran.