7 Rumus Bangun Ruang Beserta Contoh Soal dan Pembahasannya

Dalam pelajaran matematika, siswa wajib mempelajari dan memhami rumus bangun ruang. Bangun ruang sendiri dapat diartikan sebagai bangun tiga dimensi yang memiliki ruang dan dibatasi oleh sisi-sisi nya.
Bangun ruang memiliki volume, isi, dan tiga komponen, yaitu sisi rusuk, dan titik sudut. Bangun ruang memiliki berbagai macam jenis,antara lain kubus, balok, trapesium, limas, dan lain sebagainya.
Pada artikel ini, akan dibahas lebih mendalam tentang rumus bangun ruang, baik volume maupun luas permukaan, beserta contoh soalnya yang bisa dipelajari. Berikut di bawah ini rangkumannya.
Rumus Bangun Ruang
Berikut tujuh rumus bangun ruang beserta contoh soal dan pembahasannya.
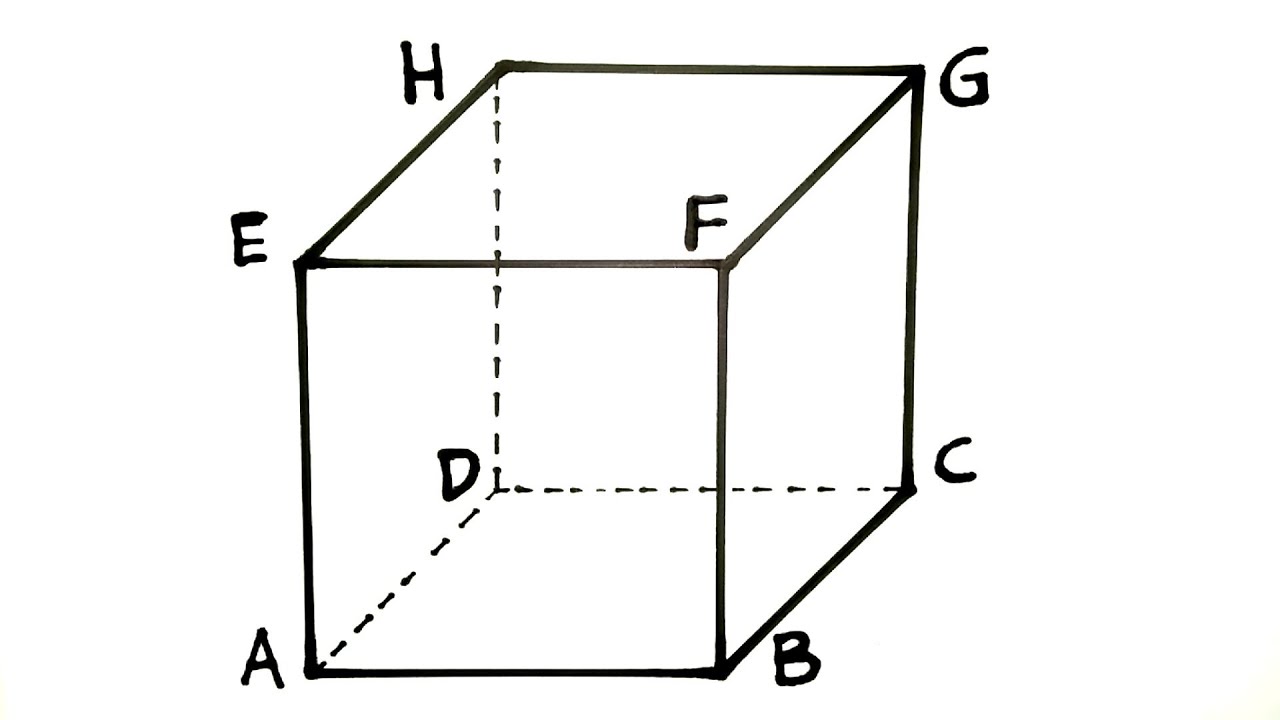
1. Kubus
Bangun ruang kubus merupakan bangun ruang yang terdiri atas 6 sisi, 12 rusuk, dan 8 titik sudut.
- Rumus volume kubus, yaitu : V = s x s x s
- Luas permukaan kubus, yaitu L = 6 x (s x s)
- Rumus keliling kubu, yaitu : K = 12 x s d.
- Luas sisi Luas salah satu sisi : L = s x s
Contoh Soal
Sebuah kotak kapur memiliki sisi 10 cm, berapa luas, keliling, dan volumenya?
Jawab:
L = 6 x s = 6 x 10 = 60 cm2.
K = 12 x s = 12 x 10 = 120 cm.
V = s x s x s = 10 x 10 x 10 = 1000 cm3.
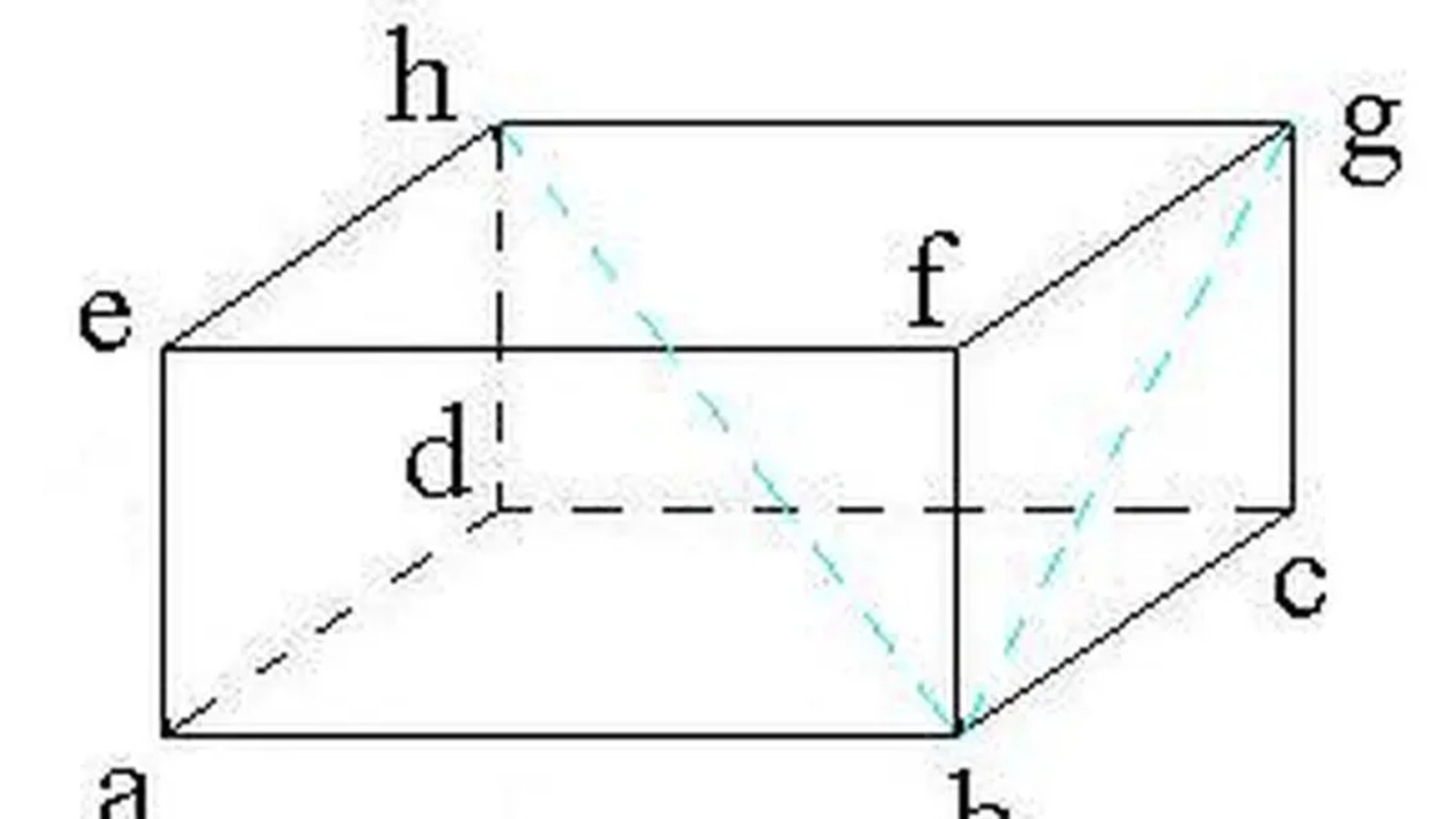
2. Balok
Balok merupakan bangun ruang yang terdiri atas 6 sisi, 12 rusuk, dan 8 titik sudut.
- Luas balok, yaitu: L = 2 x [(p x l) + (p x t) + (l x t)]
- Keliling balok = K = 4 x (p + l + t)
- Volume balok, yaitu: V = p x l x t
P merupakan panjang, l adalah lebar, K sama dengan keliling, dan t yaitu tinggi.
Contoh soal:
Sebuah bangun ruang memiliki panjang 24 cm, lebar 10 cm, dan tinggi 5 cm. Berapa volume bangun ruang tersebut?
Pembahasan:
L = 2 x [(p x l) + (p x t) + (l x t)]
= 2 x [(24 x 10) + (24 x 5) + (10 x 5)]
= 2 x [240 + 120 + 50] = 820 cm2.
K = 4 x (p + l + t) = 4 x (24 + 10 + 5) = 156cm
V = p x l x t = 24 x 10 x 5 = 1.200 cm3
3. Bola
Bola adalah bangun ruang yang permukaannya rapat dan bagian dalamnya berongga. Semua titik pada sisinya berjarak sama ke titik pusatnya.
Rumus mencari volume bola yaitu
V = 4/3 x π × r³
Keterangan:
π = 22/7 atau 3,14
r = ukuran jari-jari
Contoh soal:
Nani mendapat hadiah bola dari kakaknya. Berapa volume bola tersebut jika jari-jarinya berukuran 20 cm?
Jawaban:
Rumus bangun ruang bola adalah V = 4/3 x π × r³
V = 4/3 x 3,14 × 20³
V = 4/3 x 3,14 × 8.000
Volume bola Nani adalah 33.493,3 cm³
4. Tabung
Tabung adalah bangun ruang yang dibatasi oleh dua daerah lingkaran yang sejajar dan sama ukurannya.
Selain itu, tabung juga memiliki sebuah bidang lengkung yang berjarak sama jauh ke porosnya dan yang simetris terhadap porosnya memotong kedua daerah lingkaran tersebut tepat pada kedua daerah lingkaran itu.
Rumus volume tabung = π × r² × t
Keterangan:
r = ukuran jari-jari lingkaran
t = tinggi
Contoh soal:
Sebuah mainan berbentuk tabung diketahui memiliki ukuran jari-jari 10 cm dan tinggi 30 cm. Berapakah volume tabung itu?
Jawaban:
Cara mencari volume bangun ruang ini sama seperti sebelumnya, langsung masukkan angka yang diketahui ke dalam rumusnya.
V = π × r² × t
V = 3,14 x 10² x 30
V = 3,14 x 100 x 30
Volume tabung tersebut yaitu 9.420 cm³
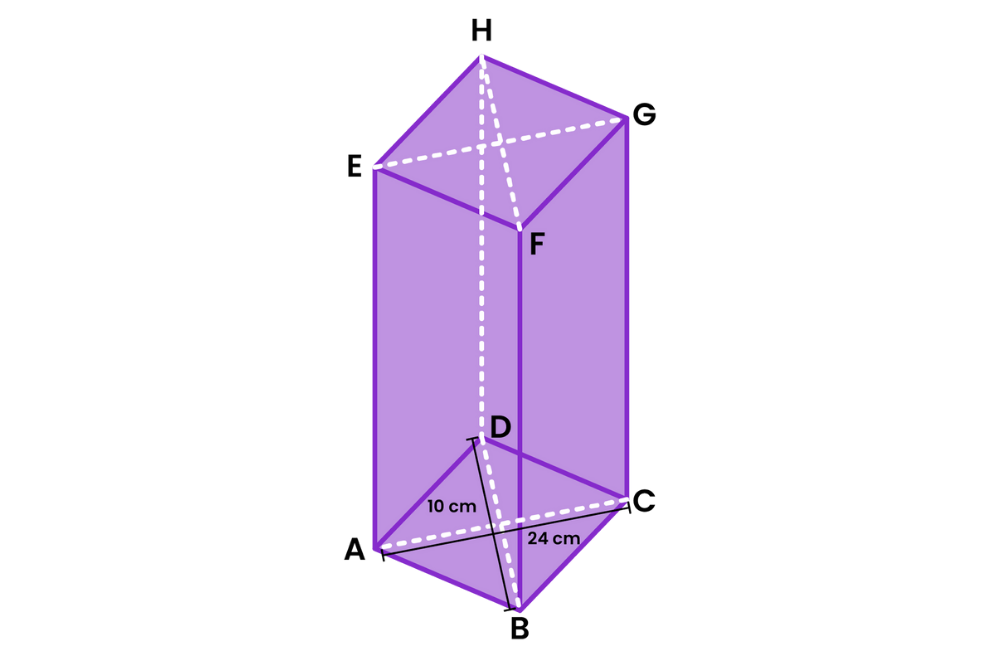
5. Prisma
Prisma adalah bangun ruang yang dibatasi oleh dua bidang segi banyak yang sejajar, kongruen, dan bidang-bidang tegak yang menghubungkan segi banyak tersebut.
Berikut rumus luas dan volume bangun ruang prisma segitiga.
- L = 2 x luas alas + luas selimut
L = luas permukaan
- luas alas = 1/2 x panjang alas x tinggi alas
- luas selimut = keliling alas x tinggi prisma
- V = luas alas x tinggi prisma
V = volume
- luas alas = 1/2 x panjang alas x tinggi alas
t = tinggi prisma
Contoh soal:
Diketahui sebuah prisma segitiga siku-siku memiliki panjang alas 3 cm, tinggi alas 4 cm, dan diagonal 5 cm, serta tinggi prisma 10 cm. Berapakah luas permukaan dan volumenya?
Jawab:
L = 2 x luas alas + luas selimut
= 2 x (1/2 x panjang alas x tinggi alas) + (keliling alas x tinggi prisma)
= 2 x (1/2 x 3 cm x 4 cm) + (3 cm + 4 cm + 5 cm x 10 cm)
= 132 cm²
V = luas alas x t
= (1/2 x panjang alas x tinggi alas) x tinggi prisma
= (1/2 x 3 cm x 4 cm) x 10 cm
= 60 cm³
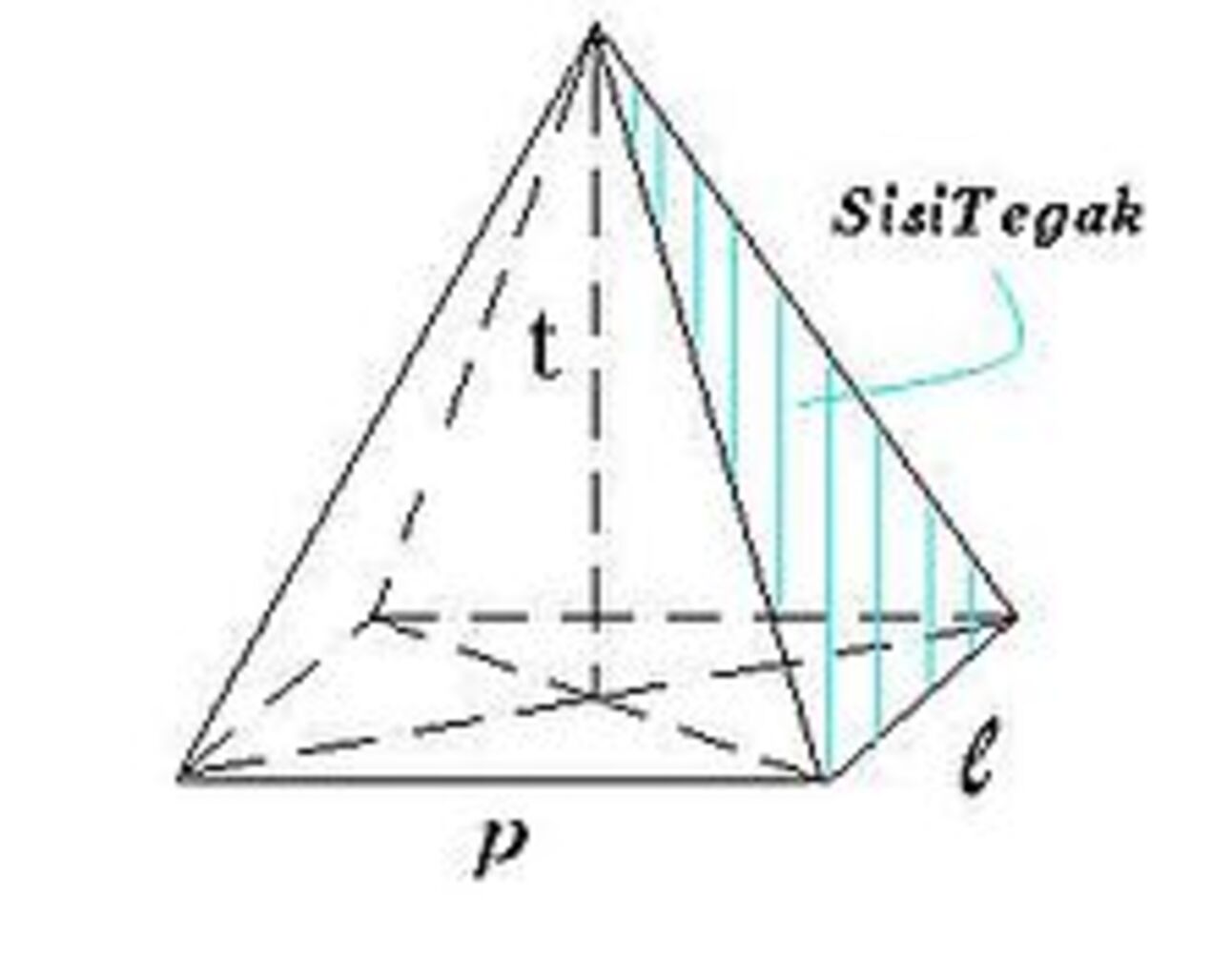
6. Limas
Limas adalah bangun ruang yang dibatasi oleh sebuah segi banyak dan segitiga-segitiga yang mempunyai titik puncak persekutuan di luar bidang segi banyak itu.
Berikut rumus luas dan volume bangun ruang limas segiempat.
- L = luas alas + jumlah luas sisi tegak
L = luas permukaan
- luas alas = sisi x sisi
- jumlah luas sisi tegak = 4 x 1/2 x sisi x tinggi segitiga sisi tegak
- V = 1/3 x s x s x t
V = volume
s = panjang sisi
t = tinggi limas
Contoh soal:
Diketahui sebuah limas segiempat memiliki panjang sisi 12 cm, tinggi limas 6 cm, dan tinggi segitiga sisi tegak 8 cm. Berapakah luas permukaan dan volumenya?
Jawab:
L = luas alas + jumlah luas sisi tegak
= (sisi x sisi) + (4 x 1/2 x sisi x tinggi segitiga sisi tegak)
= (12 cm x 12 cm) + (4 x 1/2 x 12 cm x 8 cm)
= 336 cm²
V = 1/3 x s x s x t
= 1/3 x 12 cm x 12 cm x 6 cm
= 288 cm³
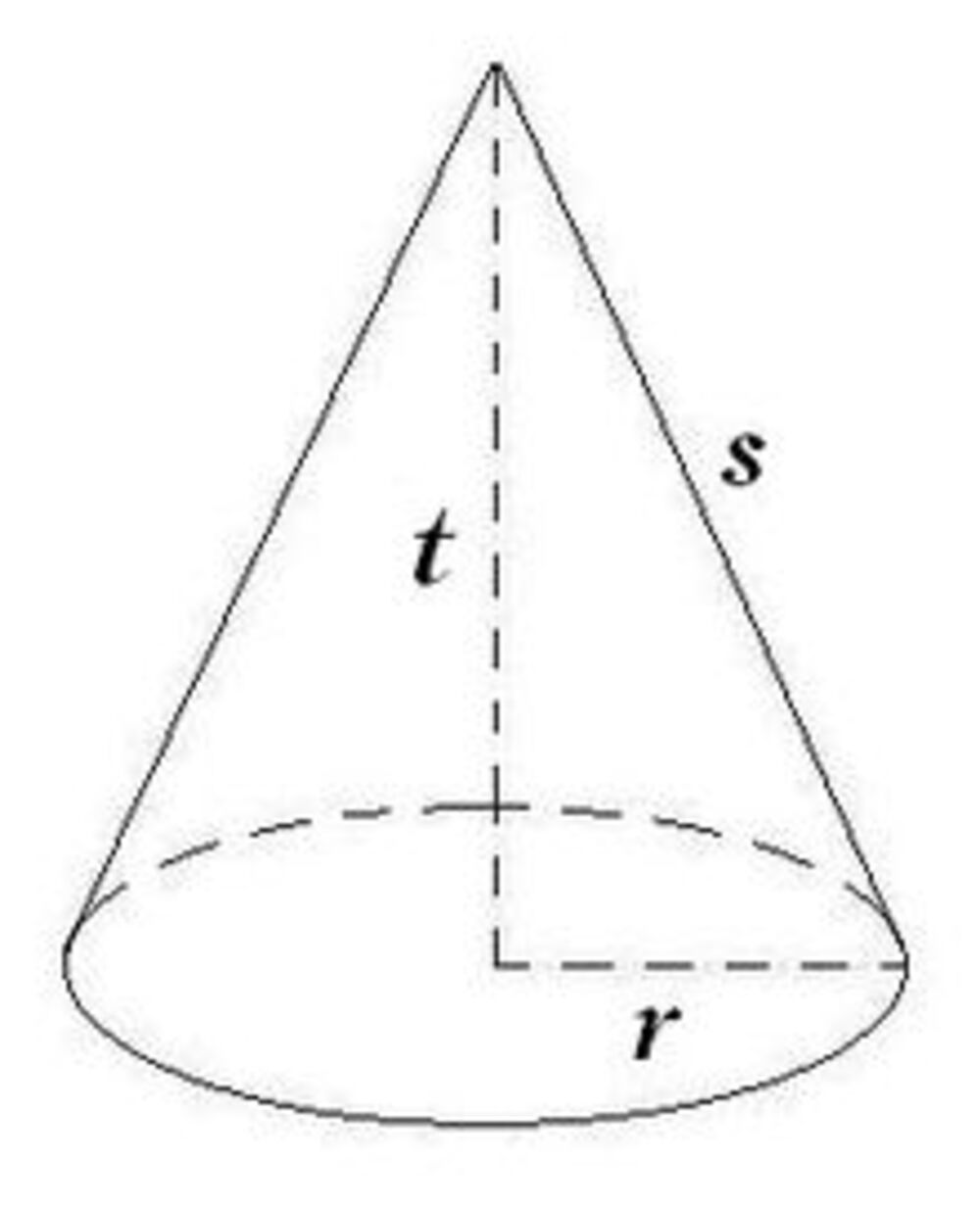
7. Kerucut
Kerucut adalah bangun ruang yang dibatasi oleh sebuah daerah lingkaran dan sebuah bidang lengkung kerucut.
Berikut rumus luas dan volume bangun ruang kerucut.
- L = (π x r x s) + (π x r x r)
L = luas permukaan
π = konstanta perbandingan keliling lingkaran dengan diameternya. Nilai π atau phi adalah 22/7 (untuk jari-jari kelipatan 7) atau 3,14 (untuk jari-jari selain kelipatan 7)
r = jari-jari
s = garis pelukis
- V = 1/3 x π x r x r x t
V = volume
π = konstanta perbandingan keliling lingkaran dengan diameternya. Nilai π atau phi adalah 22/7 (untuk jari-jari kelipatan 7) atau 3,14 (untuk jari-jari selain kelipatan 7)
r = jari-jari
t = tinggi sisi
Contoh soal:
Diketahui sebuah kerucut memiliki jari-jari 6 cm, tinggi 8 cm, dan garis pelukis 10 cm. Berapakah luas permukaan dan volumenya?
Jawab:
L = (π x r x s) + (π x r x r)
= (3,14 x 6 cm x 10 cm) + (3,14 x 6 cm x 6 cm)
= 188,4 cm² + 113,04 cm²
= 301,44 cm²
V = 1/3 x π x r x r x t
= 1/3 x 3,14 x 6 cm x 6 cm x 8 cm
= 301,44 cm³
Dengan pemahaman yang baik tentang rumus-rumus ini, Anda dapat mengatasi berbagai tugas matematika yang melibatkan bangun ruang. Berlatihlah dengan contoh soal di atas, dan Anda akan semakin percaya diri dalam menghadapi materi geometri tiga dimensi. Semoga artikel ini bermanfaat bagi Anda.