Rumus Luas Selimut Tabung dan Contoh Soalnya

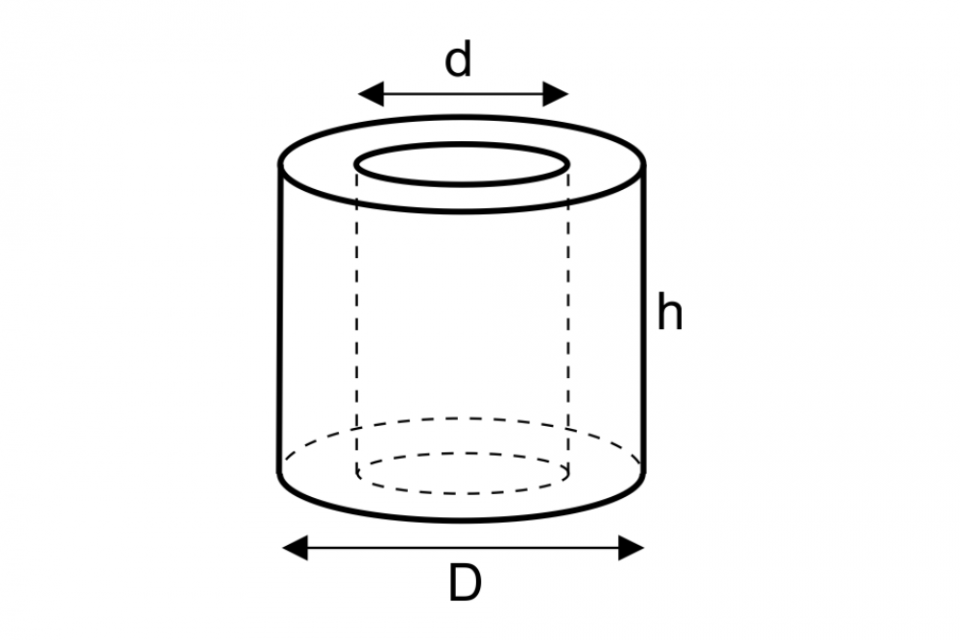
Tabung merupakan bangun ruang yang mudah ditemukan di kehidupan sehari-hari. Misalnya yaitu drum, kaleng, pipa paralon, gelas, baterai, toples, selang, dan masih banyak lagi.

Diketahui bahwa tabung merupakan salah satu jenis prisma. Hal tersebut mempengaruhi turunan rumusnya yang diketahui sekarang. Tabung juga memiliki karakteristik tertentu yang membedakannya dari bangun ruang lain, antara lain:

• Tidak mempunyai diagonal bidang.
• Tidak mempunyai diagonal ruang.
• Terdapat dua rusuk.
• Terdapat tiga sisi, yaitu alas, selimut, dan tutup.
• Terdapat dua sisi berbentuk lingkaran identik.
• Terdapat sisi berbentuk persegi panjang.
• Sisi alas dan penutup memiliki berukuran yang sama besar.
• Tinggi tabung merupakan jarak antara alas dengan tutup.

Adapun yang akan kami bahas kali ini yaitu rumus selimut tabung. Singkatnya, selimut tabung merupakan salah satu unsur yang terdapat pada bangun ruang ini. Cocok dijadikan materi pembelajaran, simak tulisan berikut ini.

Ilustrasi, tabung. (Freepik)

Apa itu Selimut Tabung?

Selimut tabung merupakan permukaan sisi yang menyelimuti tabung. Bagian ini diibaratkan tabung sebagai bangun ruang yang kerangkanya dilepaskan hingga menjadi bidang datar.

Melansir Zenius, selimut tabung diartikan sebagai sisi lengkung dalam tabung yang berada di tengah. Selimut tabung berbentuk persegi panjang. Selain itu, di bagian atas dan bawah terdapat sisi berbentuk lingkaran yang menutup tabung dan biasa disebut sebagai tutup dan alas tabung.

Rumus Luas Selimut Tabung

LS = 2 π r x t

Keterangan:

LS = Luas Selimut Tabung
π = 3,14 atau 22/7
r = jari-jari tabung
t = tinggi tabung.

Selain membahas tentang rumus luas selimut tabung, kami juga menyertakan contoh soal di bawah ini.

Contoh Soal Menghitung Selimut Tabung

Berikut ini beberapa contoh soal menghitung selimut tabung, dilansir dari Ilmusiana, Zenius, Daun, dan RPP.

1. Luas selimut tabung dengan jari-jari 30 cm dan tinggi 10 cm adalah...

Jawaban:

Diketahui:
r = 30 cm
t = 10 cm
Ditanyakan:
Luas selimut tabung...?
Penyelesaian:
Luas Selimut Tabung = 2πr x t
= 2 x 3,14 x 30 x 10
= 2 x 3,14 x 300
= 3,14 x 600
= 1.884
Jadi, luas selimut tabung adalah 1.884 cm².

2. Luas selimut tabung yang memiliki diameter 10 cm dan tinggi 4 cm adalah...

Jawaban:

Diketahui:
d = 10 cm
t = 4 cm
Ditanyakan:
Luas selimut tabung...?
Penyelesaian:
Luas Selimut Tabung = πd x t
= 3,14 x 10 x 4
= 125,6
Jadi, luas selimut tabung adalah 125,6 cm².

3. Luas selimut tabung yang alasnya berjari-jari 23 cm dan tinggi tabung 7 cm adalah...cm².

Jawaban:

Diketahui:
r = 23 cm
t = 7 cm
Ditanyakan:
Luas selimut tabung...?
Penyelesaian:
Luas Selimut Tabung = 2πr x t
= 2 x 22 / 7 x 23 x 7
= 1.012
Jadi, luas selimut tabung adalah 1.012 cm².

4. Hitung luas selimut dari sebuah tabung yang mempunyai jari-jari alas 18 cm dan tinggi 20 cm.

Jawaban:

LS = 2pr x t
2 x 3,14 x 18 x 20 = 1.056 cm²
Maka, luas selimut tabung adalah 2.260,8 cm².

5. Sebuah kue tart untuk merayakan ulang tahun berbentuk tabung dengan diameter 28 cm dan tinggi 8 cm. Jika sisi samping kue tart tersebut akan dilapisi coklat, tentukan luas permukaan kue tart yang dilapisi coklat tersebut.
Jawaban:
Diketahui:
d = 28 cm, r = 28 / 2 = 14 cm
t = 8 cm

Ditanyakan:

Luas permukaan kue dilapisi cokelat...?

Penyelesaian:

Oleh karena kue tart berbentuk tabung, maka sisi sampingnya disebut selimut. Jadi, bagian yang dilapisi coklat adalah selimut tabung. Maka, luas seluruh permukaan kue tart yang dilapisi coklat dihitung menggunakan rumus luas selimut tabung:
Luas Selimut Tabung = 2πr x t
= 2 x 22 / 7 x 14 x 8
= 704
Jadi, luas permukaan kue tart yang dilapisi coklat adalah 704 cm².

6. Diketahui sebuah tabung memiliki tinggi 25 cm dan jari jari alas 14 cm. Hitunglah luas selimut tabungnya!

Pembahasan:

Diketahui: t = 25 cm; r = 14 cm
Ditanyakan: Luas selimut = ?
Jawab:
Luas selimut tabung = 2πrt
= 2 x 22/7 x 14 x 25
= 2.200 cm²
Jadi luas selimut tabung tersebut adalah 2.200 cm².

Ilustrasi, tabung. (Freepik)

Unsur Penyusun Tabung

Selain selimut, tabung memiliki unsur lain yang menyusunnya. Berikut pembahasannya.

1. Alas dan tutup tabung

Masih mengutip Zenius, bangun ruang ini memiliki dua lingkaran sejajar dan berhadap-hadapan yang terletak pada atas dan bawah tabung. Pada bagian ini, terdapat jari-jari tabung yang ukurannya sama seperti jari-jari pada lingkaran.

2. Jari-jari tabung

Seperti yang disebutkan sebelumnya, jari-jari tabung dihitung dari jari-jari alas atau tutup tabung yang berbentuk lingkaran. Jari-jari adalah setengah dari diameter alas tabung.

3. Tinggi tabung

Tinggi tabung merupakan ukuran tabung dari atas ke bawah. Tepatnya mulai dari tutup hingga alas tabung.

Demikian pembahasan tentang rumus luas selimut tabung yang dapat dipelajari lebih lanjut. Anda dapat mengerjakan soal-soal di atas untuk melatih pemahaman dan kemampuan.