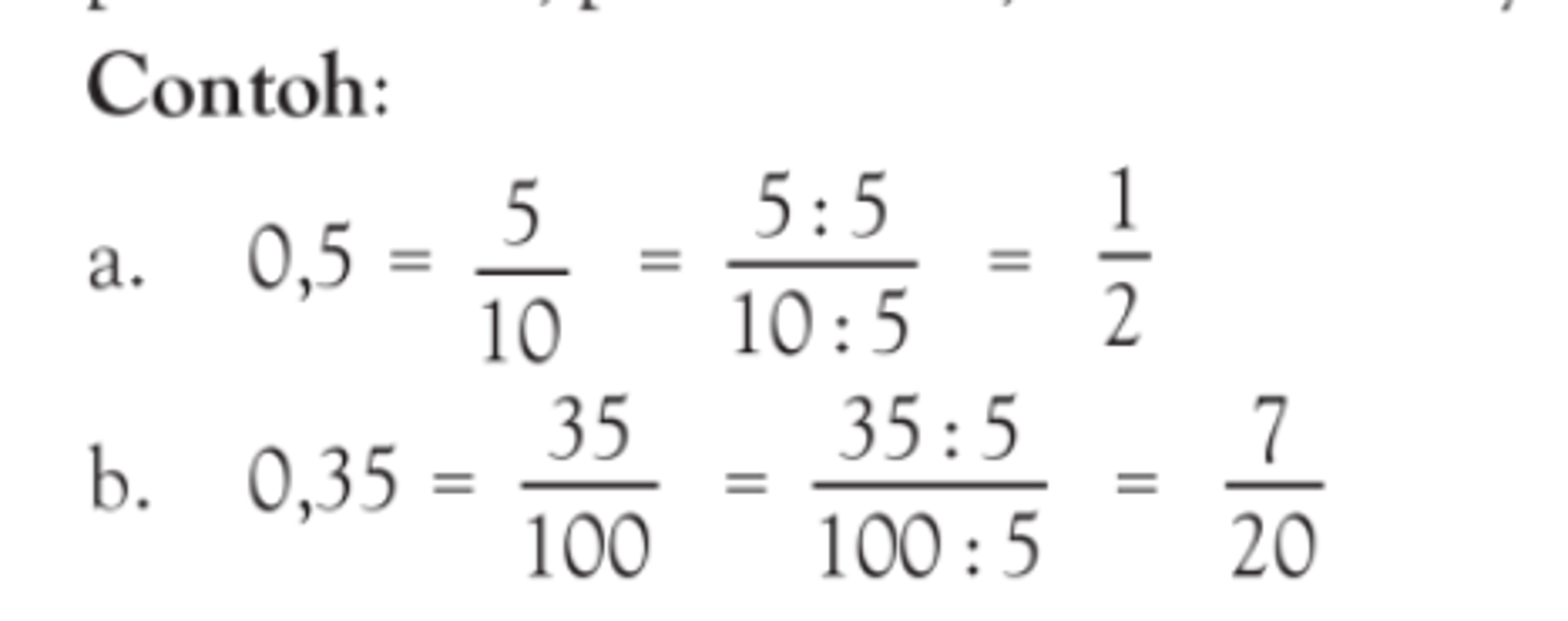Pengertian Bilangan Rasional, Sifat-sifat, dan Contoh Soalnya

Sejak bangku sekolah dasar, kita dikenalkan dengan pecahan sederhana. Dalam matematika, siswa mempelajari cara menentukan hasil operasi suatu pecahan. Kemudian penentuan operasi pecahan ini untuk menyelesaikan permasalahan sehari-hari dalam pecahan. Ternyata pecahan adalah bentuk bilangan rasional.
Dalam matematika, terdapat beberapa jenis bilangan, yakni pecahan, bilangan asli, bilangan prima, bilangan rasional, dan irasional. Berdasarkan Kamus Besar Bahasa Indonesia (KBBI), bilangan artinya satuan jumlah. Pengertian lain bilangan yaitu satuan dalam sistem matematis yang abstrak, bisa ditambah, dibagi, dan dikalikan.
Berikut penjelasan tentang bilangan rasional dan bedanya dengan bilangan irasional, serta contoh soalnya.
Pengertian Bilangan Rasional
Bilangan rasional adalah suatu bilangan bisa diubah menjadi pecahan biasa (a/b). Bilangan rasional bisa diubah menjadi pecahan desimal yang angkanya akan berhenti di suatu bilangan tertentu. Bisa juga angka akan membentuk pola pengulangan.
Misalnya pecahan ab dengan dengan b ≠ 0, a dan b termasuk bilangan bulat. Artinya semua bilangan bulat, baik itu positif, negatif, termasuk bilangan rasional. Mengapa semua bilangan bulat bisa dijadikan bilangan bulat? Karena semua bilangan bulat bisa dijadikan pecahan dengan penyebut 1. Contohnya 3 diubah menjadi 31, 7 diubah menjadi 71, dan seterusnya.
Sifat-sifat Bilangan Rasional
Berdasarkan sifatnya, bilangan rasional berlaku terhadap operasi perkalian, penjumlahan, dan gabungan perhitungan. Beberapa jenis sifat bilangan rasional yaitu sifat tertutup, komutatif, asosiatif, identitas, dan invers bilangan rasional. Berikut penjelasan lengkapnya.
1. Sifat Tertutup (Perkalian dan Penjumlahan)
a/b + c/d
a/b . c/d
2. Sifat Komutatif (Perkalian dan Penjumlahan)
a/b + c/d = c/d + a/b
a/b . c/d = c/d . a/b
3. Sifat Asosiatif
(a/b + c/d) + e/f = a/b + (c/d + e/f)
(a/b . c/d) . e/f = a/b . (c/d . e/f)
4. Sifat Distributif
a/b . (c/d + e/f) = a/b . c/d + a/b . e/f
5. Sifat Identitas
Bilangan identitas terdiri dari angka 1 atau 0-1. Operasi bilangan rasional dengan unsur identitasnya menghasilkan bilangan rasional itu sendiri.
Identitas Penjumlahan
Penjumlahan unsur identitas dan bilangan rasional akan menghasilkan bilangan rasional itu sendiri. Pada bilangan ab di mana a, b ∈ Q, berlaku:
dengan disebut sebagai unsur identitas penjumlahan
Identitas Perkalian
Perkalian unsur identitas dan bilangan rasional menghasilkan bilangan rasional itu sendiri. Pada bilangan ab di mana a, b ∈ Q, berlaku:
dengan disebut sebagai unsur identitas perkalian
6. Inversi Bilangan Rasional
Penjumlahan
Jika suatu bilangan rasional dijumlahkan dengan inversnya akan menghasilkan nilai 0. Untuk bilangan ab dimana a, b ∈ Q, memiliki invers -ab, sehingga ab+-ab=0.
Perkalian
Jika suatu bilangan rasional dikalikan dengan inversnya akan menghasilkan nilai 1. Untuk bilangan ab dimana a, b ∈ Q, memiliki invers ba, sehingga abba=1.
Perbedaan Bilangan Rasional dan Irasional
Bilangan rasional adalah bilangan yang bisa diubah menjadi pecahan bisa (a/b). Bilangan rasional bisa diubah menjadi pecahan desimal, maka angka akan berhenti di suatu bilangan tertentu. Jika angka tidak berhenti maka membentuk pola pengulangan.
Sedangkan bilangan irasional adalah bilangan yang tidak bisa diubah menjadi pecahan ab. Bilangan irasional berupa bentuk desimal dengan deret angka tidak teratur, serta bentuk akar tidak menghasilkan bilangan bulat. Contohnya angka 1,256398; 0,28759; 3; dan seterusnya.
Contoh bilangan irasional:
√6 = 2,44948974
Angka 6 jika diakarkan menghasilkan nilai 2,44948974. Artinya, bahwa nilai desimal tidak memiliki pola dan tidak berulang serta tidak berhenti.
Cara Menentukan Bilangan Rasional
1. Mengubah Pecahan ke Desimal
Cara menentukan bilangan rasional yaitu mengubahnya ke bentuk desimal. Catatan angkanya akan berhenti di suatu bilangan tertentu. Jika tidak berhenti mengalami pola pengulangan.
8/3 = 2,666666… (bilangan tersebut memiliki pola pengulangan)
3/2 = 1,5 (bilangan tersebut berhenti di suatu biangan)
2. Menyatakan dalam Pecahan
Langkah selanjutnya adalah mengubah ke pecahan. Bilangan rasional dibuktikan misalnya a/b, dimana a sebagai pembilang dan b sebagai penyebut. Suatu bilangan dapat diubah dalam bentuk pecahan jika pembilang dan penyebutnya buka angka nol (0). Artinya bilangan tersebut terbukti sebagai bilangan rasional.
Contohnya:
√16 = 4 diubah ke bentuk pecahan a/b menjadi 4/1
di mana 4 dan 1 merupakan bilangan bulat dan 1 bukan 0
√9 = 3 (Angka 3 dan 1 merupakan bilangan bulat buka 1 dan 0)
Contoh Soal Bilangan Rasional
23 + 0,023 = 23 + 0,023 =23,000 + 0,023 = 23,023
3,14 – 2,7 = 8,44 – 5,7 = 8,44 – 5,70 = 2,74
3(1/2) × 4/7 = 3(1/2) × (4/7) = (7/2) × (4/7) = (4/2) = 2
28 ÷ 1(1/4) = 28 ÷ 1(1/4) = 28 ÷ (5/4) = (112/4) ÷ (5/4) = (112/5) = 22 (2/5)
10 ÷ 1,25 = 10 ÷ 1,25 = 10 ÷ (5/4) = (40/4) ÷ (5/4) = (40/5) = 8
(1/4) = (1/4) × (25/25) = 25/100 = 0,25
(1/5) = (1/5) × (20/20) = 20/100 = 0,20
(1/25) = (1/25) × (4/4) = 4/100 = 0,04
0,6 = 6/10 = 3/5
0,04 = 4/100 = 1/25